Kullback-Leibler(KL)散度介绍

在这篇文章中，我们将探讨一种比较两个概率分布的方法，称为Kullback-Leibler散度(通常简称为KL散度)。通常在概率和统计中，我们会用更简单的近似分布来代替观察到的数据或复杂的分布。KL散度帮助我们衡量在选择近似值时损失了多少信息。

让我们从一个问题开始我们的探索。假设我们是太空科学家，正在访问一个遥远的新行星，我们发现了一种咬人的蠕虫，我们想研究它。我们发现这些蠕虫有10颗牙齿，但由于它们不停地咀嚼，很多后都掉了牙。在收集了许多样本后，我们得出了每条蠕虫牙齿数量的经验概率分布:

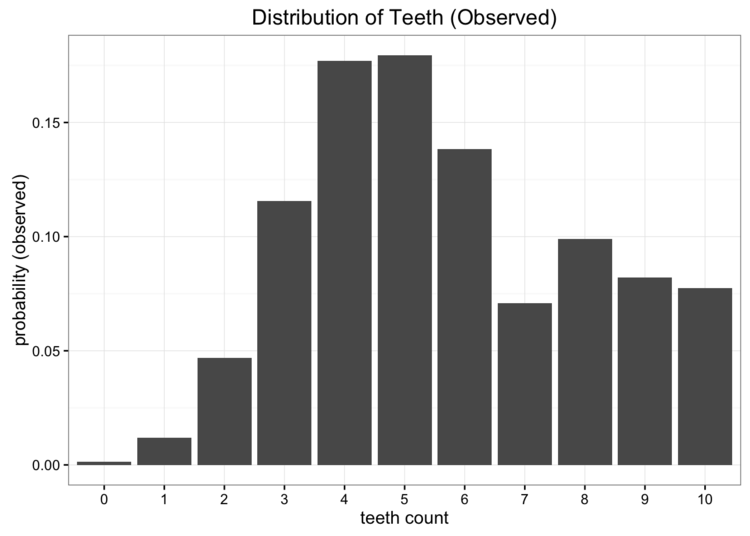
虽然这些数据很好，但我们有一个小问题。我们离地球很远，把数据寄回家很贵。我们要做的是将这些数据简化为一个只有一两个参数的简单模型。一种选择是将蠕虫牙齿的分布表示为均匀分布。我们知道有11个可能的值，我们可以指定1/11的均匀概率

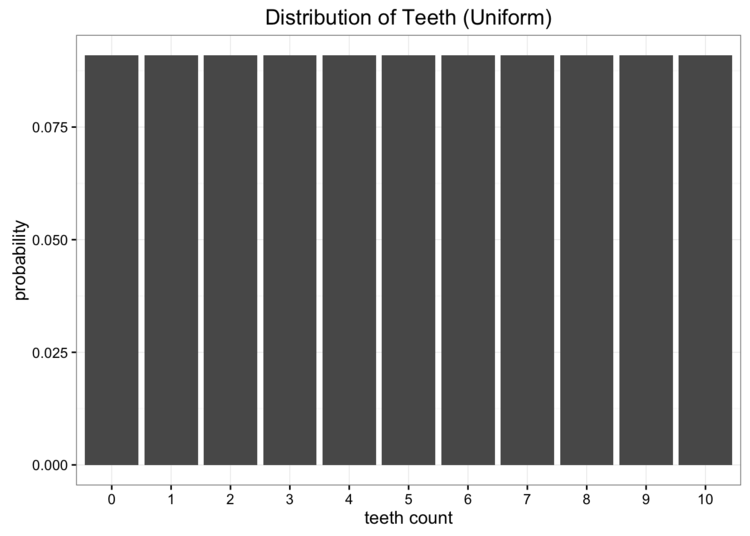
显然，我们的数据不是均匀分布的，但是看起来也不像我们所知道的任何常见分布。我们可以尝试的另一种选择是使用二项分布对数据进行建模。在这种情况下，我们要做的就是估计二项分布的概率参数。我们知道如果我们有n次试验，概率是p，那么期望就是E[x]= np。在本例中n = 10，期望值是我们数据的平均值，计算得到5.7，因此我们对p的佳估计为0.57。这将使我们得到一个二项分布，如下所示：

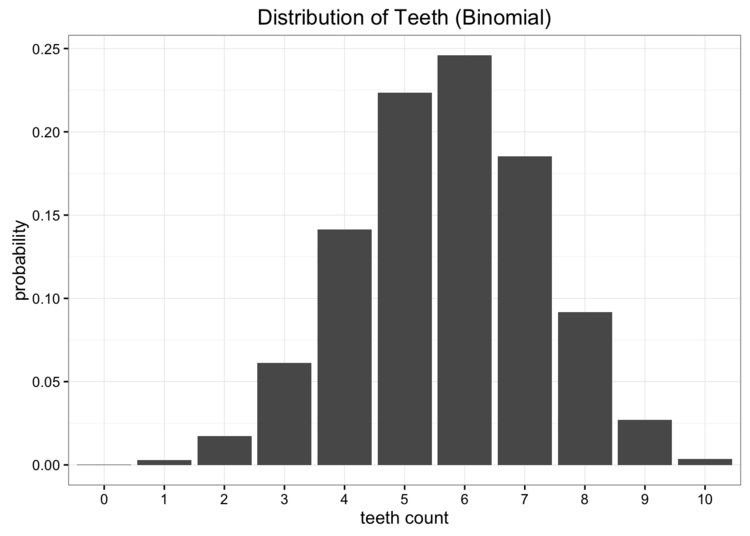
将我们的两个模型与原始数据进行比较，我们可以看出，两个都没有完美匹配原始分布，但是哪个更好？

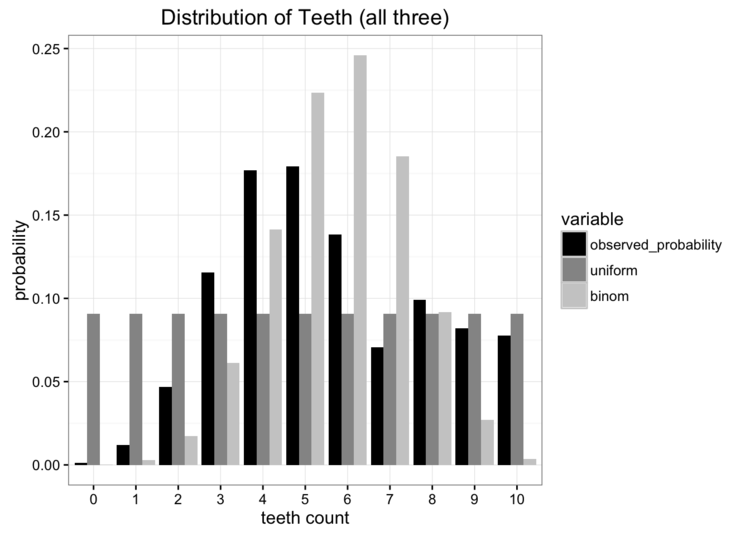
现如今有许多错误度量标准，但是我们主要关注的是必须使发送的信息量少。这两个模型都将我们的问题所需的参数量减少。好的方法是计算分布哪个保留了我们原始数据源中多的信息。这就是Kullback-Leibler散度的作用。

我们分布的熵

KL散度起源于信息论。信息论的主要目标是量化数据中有多少信息。信息论中重要的指标称为熵，通常表示为$H$。概率分布的熵的定义是：

$$H=-sum{i=1}^{N}p(xi)logp(x_i)$$

如果在我们的计算中我们使用$log_2$，我们可以把熵解释为“我们编码信息所需要的小比特数”。在这种情况下，根据我们的经验分布，信息将是每个牙齿计数的观察结果。根据我们观察到的数据，我们的概率分布的熵为3.12比特。比特的数目告诉我们，在单一情况下，我们平均需要多少比特来编码我们将观察到的牙齿数目。

熵没有告诉我们可以实现这种压缩的佳编码方案。信息的佳编码是一个非常有趣的主题，但对于理解KL散度而言不是必需的。熵的关键在于，只要知道所需位数的理论下限，我们就可以准确地量化数据中有多少信息。现在我们可以对此进行量化，当我们将观察到的分布替换为参数化的近似值时，我们丢失了多少信息。

使用KL散度测量丢失的信息

Kullback-Leibler散度只是对我们的熵公式的略微修改。不仅仅是有我们的概率分布p，还有上近似分布q。然后，我们查看每个log值的差异：

$$D{KL}(p||q)=sum{i=1}^{N}p(xi)(logp(xi)-logq(x_i))$$

本质上，我们用KL散度看的是对原始分布中的数据概率与近似分布之间的对数差的期望。再说一次，如果我们考虑$log_2$，我们可以将其解释为“我们预计有多少比特位的信息丢失”。我们可以根据期望重写公式：

$$D{KL}(p||q)=E[logp(xi)-logq(x_i)]$$

查看KL散度的更常见方法如下：

$$D{KL}(p||q)=sum{i=1}^{N}p(xi)(logfrac{p(xi)}{q(x_i)})$$

因为$loga-logb=logfrac{a}{b}$

利用KL散度，我们可以地计算出当我们近似一个分布与另一个分布时损失了多少信息。让我们回到我们的数据，看看结果如何。

比较我们的近似分布

现在我们可以继续计算两个近似分布的KL散度。对于均匀分布，我们发现：

$$D_{kl}(Observed ∣∣ Uniform)=0.338$$

对于我们的二项式近似：

$$D_{kl}(Observed ∣∣ Binomial)=0.477$$

如我们所见，使用二项式分布所损失的信息大于使用均匀分布所损失的信息。如果我们必须选择一个来代表我们的观察结果，那么好还是坚持使用均匀分布。

KL散度不是距离

将KL散度视为距离度量可能很诱人，但是我们不能使用KL散度来测量两个分布之间的距离。这是因为KL散度不是对称的。例如，如果我们将观察到的数据用作近似二项式分布的方式，我们将得到非常不同的结果：

$$D_{kl}(Binomial∣∣Observed)=0.330$$

使用KL散度进行优化

当我们选择二项分布的值时，我们通过使用与数据匹配的期望值来选择概率参数。但是，由于我们正在进行优化以大程度地减少信息丢失，因此这可能并不是选择参数的佳方法。当我们更改此参数的值时，我们可以通过查看KL散度的变化方式来仔细检查我们的工作。以下是这些值如何一起变化的图表：

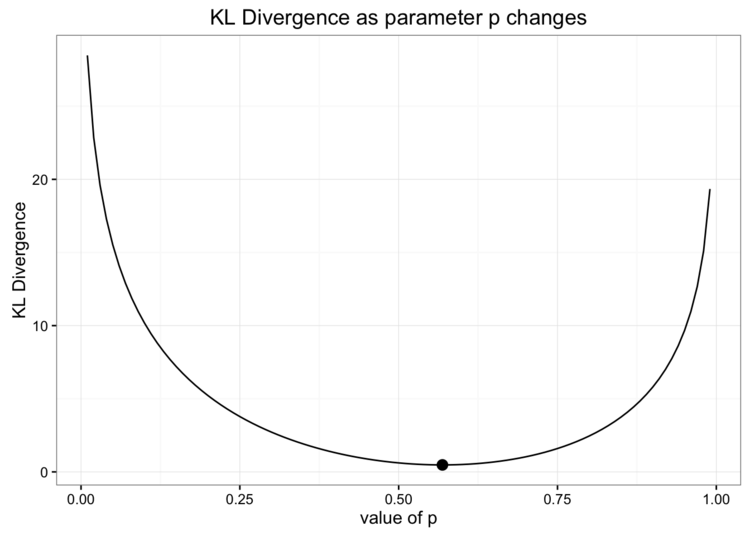
如你所见，我们对二项式分布的估计（由点标记）是使KL散度小的佳估计。

假设我们要创建一个临时分布来对数据建模。我们将数据分为两部分。0-5颗牙齿的概率和6-10颗牙齿的概率。然后，我们将使用单个参数来指定总概率分布的百分比落在分布的右侧。例如，如果我们为参数选择p=1，则6-10的概率分别为0.2，0-5组中的所有事物的概率均为0。：

$$[6,11]=frac{p}{5};[0,5]=frac{1-p}{6}$$

注意：因为 $log$在0点未定义，我们允许为零的概率是当$p(xi)=0$，可以推出$q(xi)=0$

我们如何才能找到我们组合在一起的这个奇怪模型的佳参数？我们需要做的就是像以前一样大程度地减少KL差异：

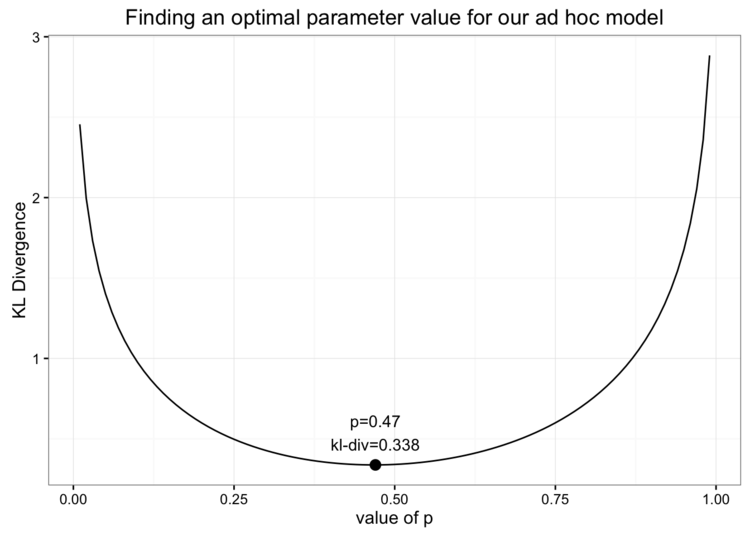
我们发现在以下情况下找到的KL散度的小值是0.338，当p = 0.47。小KL散度的值应该看起来很熟悉：它几乎与我们均匀分布得到的值相同！当我们用p的理想值绘制出我们的分布的值时，我们发现它几乎是均匀的:

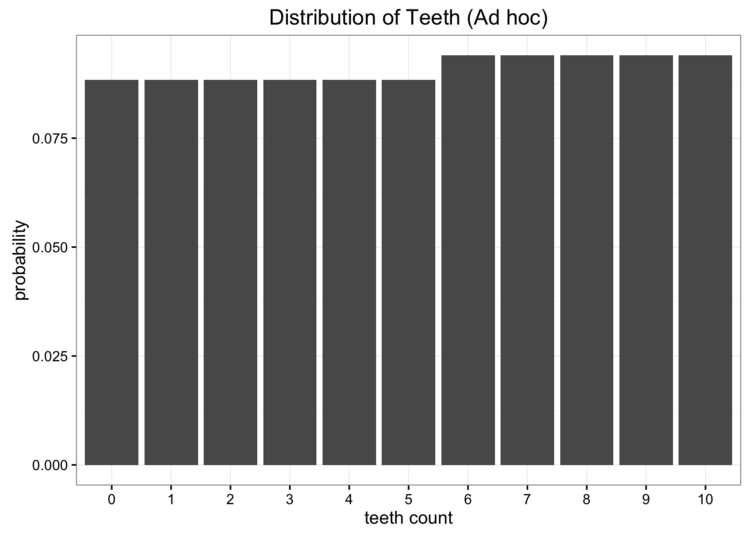
由于我们不会使用临时分布来保存任何信息，因此好使用更熟悉，更简单的模型。

这里的关键点是，我们可以将KL散度作为目标函数来找到我们可以得出的任何近似分布的优值。尽管此示例仅优化单个参数，但我们可以轻松想象将这种方法扩展到具有许多参数的高维模型。

变分自动编码器和变分贝叶斯方法

如果你熟悉神经网络，那么你可能已经猜到了上一节之后的去向。在一般的意义上，神经网络是函数近似器。这意味着你可以使用神经网络来学习各种复杂的功能。使神经网络学习的关键是使用目标函数，该函数可以告知网络运行状况。你可以通过小化目标函数的损失来训练神经网络。

如我们所见，我们可以使用KL散度来小化近似分布时的信息损失量。将KL散度与神经网络相结合，可以让我们学习非常复杂的数据近似分布。一种常见的解决方法称为“变分自编码器”，它学习了近似数据集中信息的佳方法。以下链接一个很棒的教程，深入探讨了构建变分自编码器的细节：https://arxiv.org/abs/1606.05908。

更一般的是变分贝叶斯方法领域。在其他文章中，我们看到了蒙特卡洛模拟可以有效解决一系列概率问题。尽管蒙特卡洛模拟可以帮助解决贝叶斯推理所需的许多难解积分，但即使这些方法在计算上也非常昂贵。包括变分自动编码器在内的变分贝叶斯方法使用KL散度来生成佳近似分布，从而可以对非常困难的积分进行更有效的推断。要了解有关变分推理的更多信息，请查看python的Edward库：http://edwardlib.org/。

磐创AI技术博客资源汇总站：http://docs.panchuang.net/PyTorch官方中文教程站：http://pytorch.panchuang.net/OpenCV中文官方文档： http://woshicver.com/