来源：图灵TOPIA

近日，Facebook AI宣布建立了个使用符号推理解决数学方程式的AI系统，准确率碾压Mathematica和Matla。

通过开发一种将复杂的数学表达式表示为一种语言的新方法，然后将解决方案替换序列到序列神经网络的翻译问题，研究者建立了一个在求解积分问题和一阶、二阶微分方程方面都优于传统计算的系统。

以前，这类问题被认为超出了深度学习模型的范围，因为求解复杂方程需要而不是近似。

神经网络擅长于通过近似来学习如何成功，比如识别一个特定的像素模式可能是一个狗的图像，或者一个句子在一种语言中的特征与另一种语言中的特征相匹配。

解决复杂的方程也需要处理符号数据的能力，比如公式b - 4ac = 7中的字母。这些变量不能直接相加、相乘或分割，而且只能使用传统的模式匹配或统计分析，神经网络被限制在极其简单的数学问题上。

Facebook AI表示，他们提出的解决方案是一种全新的方法，可将复杂的方程式透明语言中的句子，因此他们能够在神经机器翻译（NMT）训练模型中充分利用成熟的技术，从而将问题从本质上转化为解决方案。

为了实施此方法，他们需要开发一种将现有数学表达式分解为两种语言的语法的方法，并生成包含超过100M个配对方程式和解的大规模训练数据集。

当面对成千上万个不可见的表达式时，这些方程并不是训练数据的一部分，研究者的模型比传统的代数方程求解软件，如Maple、Mathematica和Matlab，在速度和准确性上都有显著提高。

这项研究不仅证明了深度学习可以用于符号推理，还表明神经网络有潜力处理更广泛的任务，包括那些通常与模式识别无关的任务。研究者正在分享研究者方法的细节，以及帮助其他人生成类似训练集的方法。

应用神经机器翻译（NMT）的新方法

特别擅长符号数学的人往往依赖一种直觉。他们对给定问题的解决方案应该有什么样的感觉，例如观察到，如果要积分的函数中存在余弦，则其积分中可能存在正弦，然后进行必要的工作来证明。

通过训练一个模型来检测符号方程的模式，研究者相信神经网络可以拼凑出解决方案的线索，这与人类基于直觉的复杂问题处理方法大致相似。

因此，研究者开始探索作为一个NMT问题的符号推理，其中一个模型可以根据问题的实例及其匹配的解决方案来预测可能的解决方案。

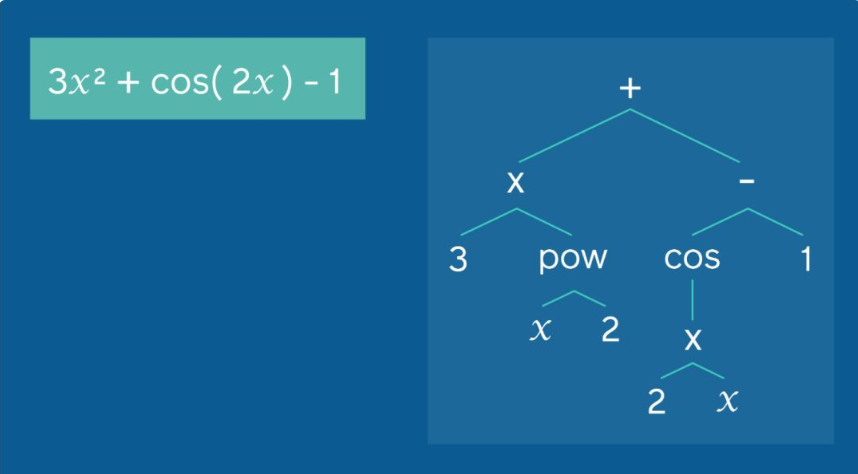
研究者的方法如何将一个现有的方程(左侧)扩展为一个表达式树，该表达式树可以作为转换模型的输入。对于这个方程，输入到研究者模型中的前序序列是:(+，乘以，3，幂，x, 2，-，cos，乘以，2,x, 1)

为了用神经网络实现这个应用，研究者需要一种表示数学表达式的新方法。NMT系统通常是序列到序列(seq2seq)模型，使用单词序列作为输入，并输出新的序列，允许它们翻译完整的句子而不是单个单词。

研究者使用了两步的方法来将其应用于符号方程。首先，研究者开发了一种有效地解包方程的方法，将方程以树枝状的分支结构展开，然后将其扩展成与seq2seq模型兼容的序列。

常量和变量充当叶子，而操作符(如加号和减号)和函数是连接树的分支的内部节点。

虽然它可能看起来不像传统语言，但以这种方式组织表达式为等式提供了一种类似于语言的语法——数字和变量是名词，而操作符是动词。

研究者的方法使NMT模型能够学习将给定树结构问题的模式与其匹配解决方案(也表示为树)进行对齐，类似于将一种语言中的一个句子与其已确认的翻译进行匹配。

这种方法允许研究者利用强大的、即时可用的seq2seq NMT模型，将单词序列替换为符号序列。

建立新的训练数据集

虽然研究者的表达式树语法使NMT模型在理论上能够有效地将复杂的数学问题转化为解决方案，但是训练这样的模型需要大量的示例。

因为在研究者关注的两类问题中（积分和微分方程）一个随机产生的问题并不总是有一个解，研究者不能简单地收集方程并把它们输入系统。

研究者需要生成一个全新的训练集，其中包含重新构造为模型可读表达式树的已解方程示例。

这就产生了“问题-解决方案”对，类似于在不同语言之间翻译的句子语料库。研究者的数据集也必须比之前使用的训练数据大得多，之前的研究试图在数千个例子上训练系统。

由于神经网络通常在拥有更多训练数据时表现更好，所以研究者创建了一个包含数百万个示例的集合。

构建这个数据集需要研究者合并一系列数据清理和生成技术。例如，对于符号积分方程，研究者改变了翻译方法:不是生成问题并找到它们的解，而是生成解并找到它们的问题(它们的导数)，这是一个更简单的任务。

这种从其解决方案中产生问题的方法，使得创建数百万个集成示例成为可能。研究者得到的受翻译启发的数据集由大约100万个成对的例子组成，其中包含积分问题的子集以及一阶和二阶微分方程。

研究者使用此数据集来训练具有8个关注头和6个层的seq2seq transformer模型。transformer 通常用于翻译任务，而研究者的网络旨在预测各种方程式的解决方案，例如确定给定函数的原语。

为了评估模型的性能，研究者向模型提供了5,000种的表达式，从而迫使系统识别出训练中未出现的方程式中的模式。

研究者的模型在解决积分问题时的准确度为99.7％，对于一阶和二阶微分方程，其准确度分别为94％和81.2％。这些结果超出了研究者测试的所有三个传统方程求解器的结果。

Mathematica的结果欠佳，在相同的积分问题上准确度为84％，对于微分方程结果的准确度为77.2％和61.6％。

研究者的模型还可以在不到0.5秒的时间内返回大多数预测，而其他系统则需要几分钟才能找到解决方案，有时甚至会完全超时。

研究者的模型将左边的方程作为输入，能够在不到一秒的时间内找到正确的解(如右边所示)。但是Mathematica和Matlab都无法解出这些方程.

将生成的解决方案与参考解决方案进行比较，可以方便而准确地验证结果。但研究者的模型也能产生一个给定方程的多个解。这类似于机器翻译，有很多方法可以翻译输入的句子。

会解方程的AI，下一步会做什么？

研究者的模型目前处理的是单变量问题，研究者计划将其扩展到多变量方程。这种方法也可以应用于其他基于数学和逻辑的领域，如物理，这可能会帮助科学家进行更广泛的工作。

但研究者的系统对神经网络的研究和使用有着更广泛的意义。可以在以前行不通的地方使用深度学习的方法去解决，这项工作表明，其他任务可能会受益于人工智能。

无论是通过将NLP技术进一步应用到传统上与语言无关的领域，还是通过在新任务或看似无关的任务中对模式识别进行更开放的探索，神经网络的限制可能是想象力的限制，而不是技术的限制。

来源：新智元 

原文链接：

https://ai.facebook.com/blog/using-neural-networks-to-solve-advanced-mathematics-equations/