模型三要素
为了将事物和问题转化为优化问题数学模型我们需要考虑三个要素:因素变量、约束条件和目标函数。我们根据事物和问题先找到影响模型的所有因素变量,然后再根据目的建立一个目标函数用来衡量系统的效果,后还要找到客观的限制条件并作为模型的约束。
如上公式,实际问题的因素变量其实可以看成是一个n维向量,向量的每个元素都是实数。f0(x)是我们构建的目标函数,我们的目标就是小化该函数(大化的情况其实也可以转化为小化的情况)。fi(x)和hj(x)作为约束函数,分不等式约束和等式约束两类,约束函数用来限制可能空间,如果不存在约束则不需要约束函数。
人工智能的优化
优化与人工智能有什么关系呢?可以这样说:人工智能在本质上也是一个优化过程,对于我们要实现的智能,也是通过学习以求得优解。这是一个总的大框架,人工智能的问题到后几乎都是回到优解问题。
不管是传统的机器学习还是大热的深度学习,亦或是大有潜力的强化学习,它们的基础核心思想都可以提升到优化问题。

有约束优化
前面提到过,优化问题可能存在约束也可能不存在约束,而且有约束的情况比无约束的情况更加复杂。约束又可以分为不等式约束和等式约束两类,约束的作用就是将优解的可能空间限制在某些区域。
纵使有了约束情况更加复杂,但我们还是有数学工具可以解决的。对于等式约束的情况,可以引入拉格朗日乘子来解决,可以将原来的目标函数和约束函数一起转化为拉格朗日函数。拉格朗日函数与原来的目标函数拥有共同的优解,所以只要求解拉格朗日函数的优解即可。对于不等式约束的情况,处理的方法也类似,只是需要额外满足KKT条件。
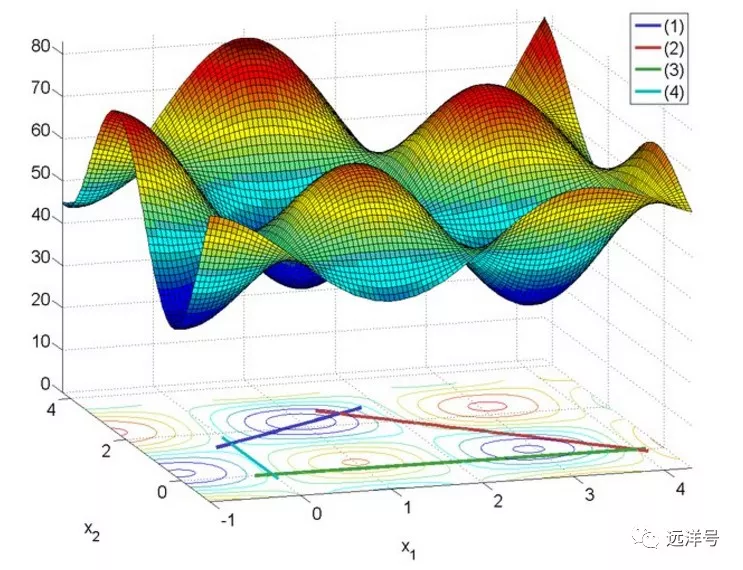
以下图为例,假设一共有四个约束条件,它们共同的限制区域为四条不同颜色限定的一个区域。假如上半部分为问题优解的所有可能空间,而经过约束条件限制后则在区域中。
无约束优化
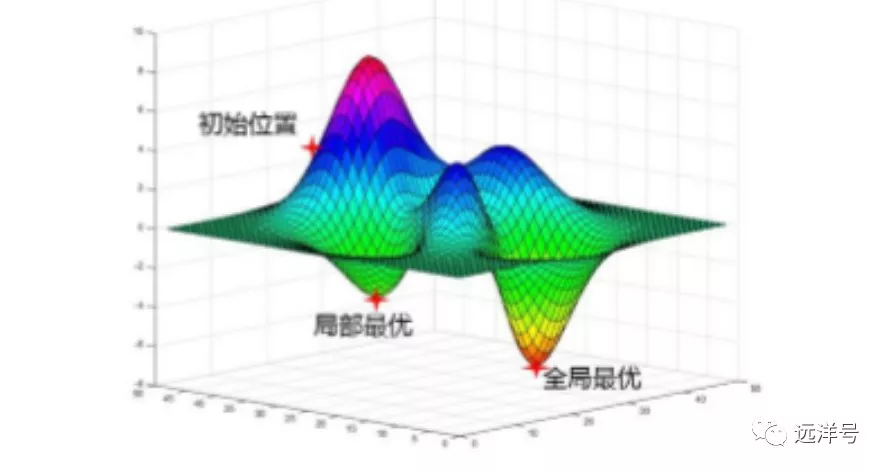
无约束的情况一般采用梯度下降法来寻找优解,所谓梯度是一个向量,梯度的方向就是函数在某点增长快的方向,梯度的模为方向导数的大值。而梯度下降的方向就是梯度的反方向,简单地看,梯度下降就好比站在一座山的某个位置上,往周围各个方向跨出相同步幅的一步,能够快下降的方向。
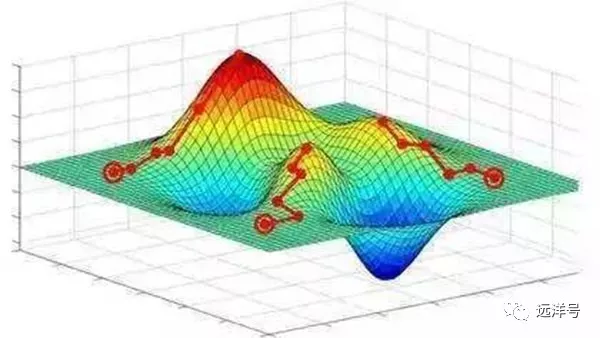
此外,采用梯度下降法寻找优解时有可能会找到局部优解,一旦陷入局部优后则可能无法跳出来继续寻找全局优。所以局部优问题也需要考虑,工程上存在专门的方法用于防止掉进局部优解。但有时局部优解和全局优解差别可能不会很大,而寻找全局优将会花费很高的代价,此时可以不必关注是否为全局优。
本公众号专注于人工智能、读书与感想、聊聊数学、计算机科学、分布式、机器学习、深度学习、自然语言处理、算法与数据结构、Java深度、Tomcat内核等。

