1. 背景
这是阅读微软在 ICDE 2013 的论文《The Bw-Tree: A B-tree for New Hardware Platforms》的笔记。
论文主要阐述了一个高性能的 atomic record stores (ARSs) 系统的实现,也就是提供原子 key-value 访问接口的系统。主要是提出了 Bw-tree ,用于解决在 new hardware platfoms 下所遇到的挑战:
- 由于生产工艺的限制,现在的 CPU 多核发展
(1)多核可以实现高的并发度,但是多核下数据访问通过在 latch 保护下的进行的,然后 latch 会带来竞争,尽管 latch 本身不慢,但是在竞争激烈的场景下,latch 导致的阻塞切出将让多核性能很难线性扩展,如下图,摘自《Java 并发编程实践》,可以很好的说明这一点;

(2)好的多核性能是建立在高的 Cache hit ratios 上,Cache miss 严重也将导致严重的性能下降,这里特别指出,memory update in place 将导致 Cache invalidations。
为解决上面两个问题,Bw-tree 设计上分别实现了两个特性:(1)latch-free,确保多核高并发的性能的 scalability;(2)通过 “delta” updates 来避免了 update in place,从而保护了之前 page 的 Cache line
新的存储设备(flash storage)
我们通常所说的 SSD 都是 flash ssd,都是 flash 作为存储介质的;flash storage 性能好,表现为高的 iops,低 latency;但是由于 SSD FTL 的缘故,顺序 write 的性能仍优于随机写 (这里先给结论,后面单独写一篇关于 SSD 原理介绍的文章,分析为什么顺序 write 性能好于随机写)。所以在Bw-tree的 flash storage 采用 log structured store (LSS) ,这样可以将随机写转化成批量的顺序写,充分发挥 ssd 顺序写性能依然优于随机写的特性
2. Bw-tree 架构
本小节描述 Bw-tree 的整体架构,如下图所示:
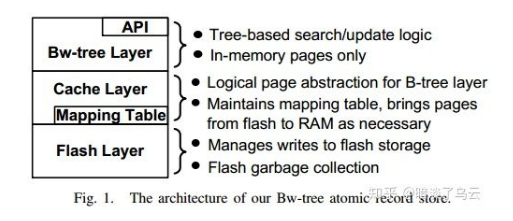
- Bw-tree layer
索引层,是一棵 B 树的扩展 bw-tree,常驻在内存中
- Cache layer
这里主要是一个 mapping table ,主要是维护了 logical ”page identifier”(PID)到物理机 page 的映射,这个物理的 page 可能是内存的 page,也可能是盘上的 page(a flash offset 即可)。这个方案其实和 ssd 中 FTL 的 Address Translation 思路是一样的,也就是 mapping 机制。这个其实也是 latch-free 的 delta update 的基础。
- Flash layer
负责数据落盘部分
3. Bw-tree 设计
3.1. 弹性虚拟页(Elastic Virtual Pages)
既然被称之为 Bw-tree,就是因为其实 B-tree 的一种,Bw-tree 主要是在 B+ 树上做了一些扩展,在介绍 Bw-tree 之前,首先介绍下 B+ 树(如下是一课 B+ 树):

这幅图来自于 https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html 自动生成的,很有意思,这也是从文献 [2] 知道的,其实本小节也是主要 copy 自文献 [2]。
B+-Tree 的特性有:
- 所有记录都在叶子节点(节点也被称为页)上,并且是顺序存放的
- 每个非叶子节点包含关键字(references)与孩子指针
- 叶子节点有一个指向左右兄弟的指针,方便顺序遍历数据
数据库一般都是使用的 B+ 树,其具有良好的 read 和 range scan 能力,但是写入的性能不是特别好,因为节点的合并和分裂会产生大量的随机读写。
Bw-tree
Bw-Tree 在 B+-Tree的基础上添加了:
- low/high key,用来标明本节点以及子节点的数据范围
- 每个节点(包括叶子节点和中间节点)都有一个 side pointer 指向其右面的兄弟节点
叶子节点是一个逻辑的 page,不像 B+ 树指向真实的数据,真实的数据是通过 mapping table 这个中间层来找到实际的物理机 page,这个也是 Bw-tree 实现 latch-free 的基础
3.1. Delta Update Page
tree latch-free 的基本思路,我们知道修改一个 page,如果是 update in place,那么肯定需要加锁,且会导致 Cache invalidations。Bw-tree 思路很巧妙,其不是原地更新 page,而是如下 Fig. 2. (a):
- 将 update 写入 delta page 中,也就是图中的 delta D,并且让 delta D page 指向 Page P
- 然后通过 cas 原子操作让 LPID P 指向新的 delta page

这样 write 完全是 latch-free,read 只需要通过 delta D page 和 Page P 就能读到新的数据。其实这种 delta page 在有些系统里面被称为 shadow,也是用来优化写入的。
3.2. Page Consolidation
由于是 delta update 的,所以 read 上可能需要 merge delta page 和 原始 page ,所以对 read 的性能是由一定影响的,而且随着 update 的增加,整个 pages 链也会越来越长,所以整个 pages 链需要定期的合并,一旦整个 pages 链长度超过一定的阈值就会触发合并。
合并的方法也非常简单(如上图 Fig.2. (b)):
- 分配一个 new page
- 将整个 pages 链上的 page merge 结果写入 new page 中
- 通过 cas 操作修改 mapping table,一旦 cas 操作成功,这些 pages 就可以删除,是通过 garbage collection 来做的
3.3. Garbage Collection
在无锁数据结构中不能够独占的问题访问一个共享的数据,那么意味着在有线程 update 某个 page 的时候,是允许其他的 reader (一个或者多个)访问这个 page 的。例如上面的 Page consolidation 在完全 page consolidation 之后就会删除那些过时的 page,而这个时候 reader 线程正在 read 这个 pages 链上的数据。这种情况下,删除需要格外小心。在 Bw-tree 中通过引入 “epoch" 的概念,来保护对象避免在使用前被提前释放的机制 [3、4],这块不是很了解,后面再单独研究研究 ???
3.4. Node Split
整个过程也是 latch-free 的,其大致的思路也是类似于 delta update

上图为将 node P split 为 P 和 Q
- 创建 node Q,并让其指向 right sibling R
- 创建 split delta page 分裂 P 和 Q,split delta 中标明该节点已经分裂,其中包含了分裂点,从而能够分别去访问 P 和 Q
- 更新 parent,通过 delta 增量原子修改 index,使用访问 Q 可以直接访问到 Q 上,而不会在落在 P 上了
3.5. Node Merge
整个过程也是 latch-free 的,其大致的思路也是类似于 delta update,Node merge 还有些疑问的地方 ?
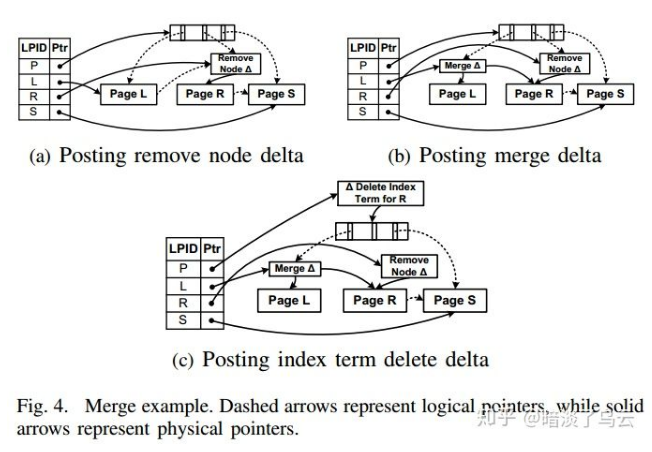
上图为 merge L 和 R,主要步骤如下:
- 通过 delta 标记删除 R;
- 通过 delta merge L 和 R,这个时候 delta 中对 L 和 R 都有指向
- 更新 parent,通过 delta 在 parent 标记删除 R,这样访问 R 就直接通过 parent 访问了
上面三步完成之后,merge 才算成功;但是上述过程并非原子的,所以会存在一些问题:
删除 R 之后到更新 parent 之间,R 如何访问的问题 ?因为访问 R 是从 parent 搜索下来的,在第 2 步更新 L 之后仍不能访问到 R 的数据,因为这个时候从 parent 访问 R,R 是被标记删除的 ???
4. 总结
Bw-tree 的 latch-free 的核心已经分析完了,但是仍有很多细节,后续再单独整体出来分析。
Notes
水平和时间有限,论文很多细节没看那么细,难免有错误和理解不到位的地方,欢迎指出和交流~
参考文献
[1]. Levandoski J J, Lomet D B, Sengupta S. The Bw-Tree: A B-tree for new hardware platforms[C]// IEEE International Conference on Data Engineering. IEEE Computer Society, 2013:302-313.
[2]. Bw-Tree:在新硬件平台上的新B-Tree
[3]. Bw-Tree技术解读. https://zhuanlan.zhihu.com/p/29314464
[4]. khizmax Lock-free Data Structures. The Inside. Memory Management Schemes
