先吐槽：
是的，就是这些等高线图，配合一个方框♦️一个圆圈⭕️ 。大多数博客都是摆上这么一张图就希望读者能够理解，这些图看似形象地不得了，吸引我们去看，结果看半天还是一头雾水。
个画出这种图的人，一定是高手，是神，因为他深刻掌握了L1和L2的精髓。但是，由于是神，他便离凡人远了些，这个图就是典型的“看似生动形象，实则高高在上”的图。
其实，只要对这些图，多画几笔，多讲几句话，我们就可以很容易理解了。下面我来给出我画的图，个人觉得更容易理解。
首先写出L1正则化和L2正则化的公式：
用等高线展示L1，L2正则化的正确姿势
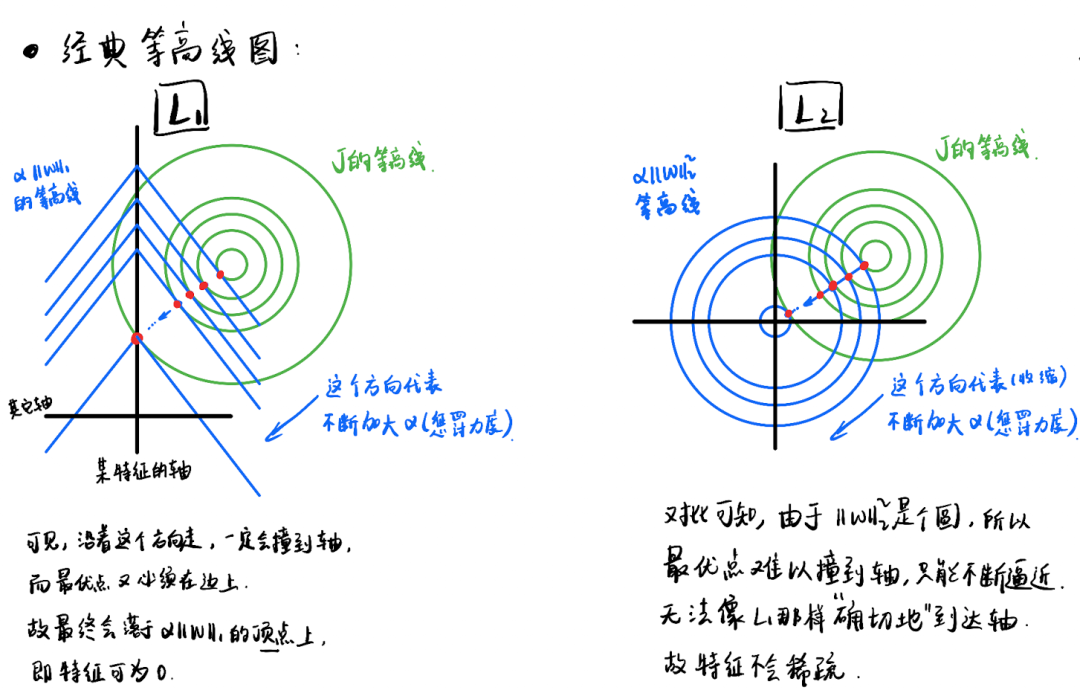
图中：
蓝色的一层层的线，代表正则项的等高线，对于L1，它是菱形的，对于L2，它是圆形的； 绿色的一层层的圆圈，代表原始损失函数的等高线图； 黑色的是坐标轴，这里展示的是二维特征的坐标轴。
关键的关键：
蓝色的等高线和绿色的等高线，分别代表了两个优化问题。对原始的损失函数J添加了正则像之后，优化问题就变成了两个子优化问题的博弈。 当J和正则项之和小时，上述的博弈取得平衡。而此时平衡点一定是相切点/端点。相切点的具体位置，取决于正则项的惩罚力度，也就是公式里的。每一个平衡点，对应着一个的设置。
可以想象：当惩罚力度大时，蓝色的线希望扯着绿色的线，往靠近坐标轴的方向移动，而惩罚力度小时，绿色的线希望扯着蓝色的线，往远离坐标轴的方向移动。
那么就好理解了，我们可以发现：
对于L1正则化，蓝线和绿线的相切点，随着蓝线不断靠近坐标轴，早晚会碰到坐标轴，抵达坐标轴之后，优点会保持在L1等高线的端点处，依然在坐标轴上，故某个特征的值会变为0。 而L2的相切点则只能无限接近坐标轴，惩罚力度再大，都到不了0。
上面这个图还是复杂了点儿，能不能分解/分步一下？
当然，真正让我彻底理解的，是当我画出下面这个图的时候：
图中展示的都是达到优的时候的两个等高线的关系。图注都写在图片里了，随着的增大，L1的蓝色的方框不断缩小，拉扯着J的绿色圆圈变大，第三张子图的时候，优点到达了L1的顶点，后面如果继续增大的话，优点会沿着纵坐标往下滑。所以，当超过某个阈值的时候，优解中的w1就会总等于0.
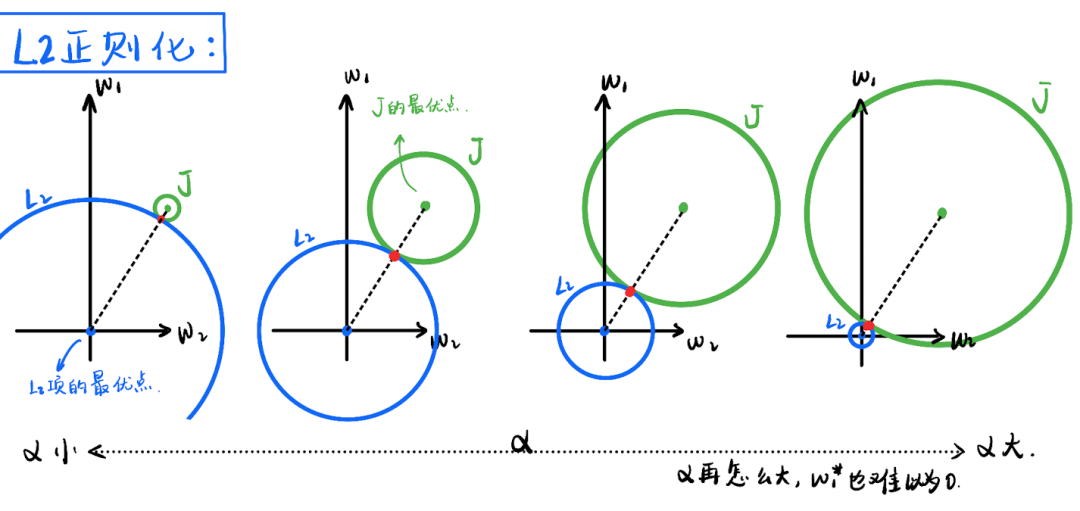L2理解起来就简单多了，两个圆一直都是相切的状态，切点永远到不了原点，也就没法让某个特征等于0。
这两张图，才真正展示了一般情况下的L1和L2正则化的特点，解释了为什么L1正则化会导致稀疏解。
后辅以推导
只有从直觉上，道理上理解了L1和L2的特点，我们再去用数学推导才有意义。
要看是否会导致稀疏解，我们可以看0附近的导数是否导致0是其邻域内的极值点：
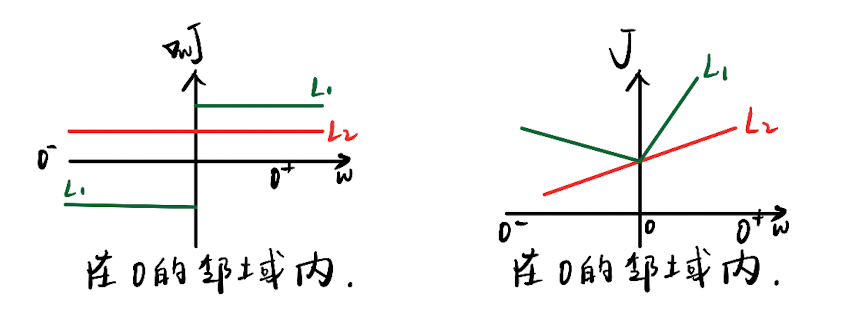
上面的推导表明，对于L1，0的邻域内，存在某种条件，使得导数先负后正，即函数先减后增，所以0是极值点。而条件是：原损失函数J在某参数为0处的导数在范围内。这个条件，说直白一点就是有没有某特征对损失函数影响不大。
而L2在0处的导数，就等于J在0处的导数。只有当原始优化问题的优解本身就是稀疏解的时候，才会使得该参数为0，而这个显然不常见。
后的后补充一句，前面我一直说的“导致”稀疏解，搞的好像稀疏解是某种不好的后果一样，不是的。其实L1这个特点，经常被用来进行特征选择，因为它可以找出那些不重要的特征。
- EOF -
