本文始发于个人公众号:TechFlow,原创不易,求个关注
今天是分布式系统的第九篇文章。
今天给大家分享的内容是LSM树,它的英文是Log-structed Merge-tree。看着有些发怵,但其实它的原理不难,和B树相比简直算是小儿科了。
并且这也是一个非常经典的数据结构,并且在大数据系统当中有非常广泛的应用。有许多耳熟能详的经典系统,底层就是基于LSM树实现的。因此,今天就和大家一起来深入学习一下它的原理。
背景知识
首先,我们先从背景知识开始。我们之前介绍B+树的时候说过,B+树和B树大的不同就是将所有的数据都放在了叶子节点。从而优化了我们批量插入以及批量查询的效率,而优化的核心逻辑就是因为无论是什么存储介质,顺序存储的效率一定要比随机存储更高,并且高的还不是一点半点。这个已经算是老生常谈了,如果我没记错的话,这已经是我第三次在文章当中提到这一点了。
我近看到了一张图,很好地阐述了随机读取和顺序读取两者的效率差,我们来看下面这张图。其中绿色的部分表示硬盘顺序读取的大速度,而红色表示随机读取时的速度。
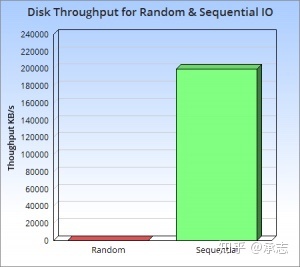
我们看下纵坐标就知道,这两者差的不是一点半点,已经有数量级的差距了。而且还不止是一个数量级,至少相差了三个数量级,显然这是非常恐怖的。另外,这个差距并不只是在传统的机械硬盘上存在,即使是现在比较先进的SSD固态硬盘上,也一样存在。也就是说这个差距是介质无关的。
直观优化
既然随机读取和顺序读取的效率差了这么多,不由得不让人心动。如果能够发明一个数据结构可以充分地利用上这一点,那么我们的系统对数据的吞吐能力一定可以再上一个台阶。对于许多科技公司而言,尤其是大数据公司,因为数据量带来的机器开销的费用占据了日常支出的大头。如果能够很好地解决这个问题,显然可以节约大量的资源。
一个朴素的想法就是将所有的读写都设计成顺序读写,比如日志系统就是一个典型的例子。在我们记录日志的时候,总是添加在文件的末尾,而不会插入在文件的中间。由于我们总是添加在文件末尾,在磁盘上这是一个顺序的读写。但我们把读写都设计成顺序的,也就意味着我们当我们要查找的内容在文件中间的时候,我们必须要读入文件中的所有内容。
这个思路应用广泛的地方有两个,一个是数据库的日志当中。在我们用数据库执行写入或者修改操作的时候,数据库会将所有的变更写成log记录下来。还有一处是消息系统的中间件,比如kafka。
但是在复杂的增删查改的场景当中,尤其是涉及到批量读写的场景,简单的文件顺序读写就不能满足需求了。当然我们可以引入哈希表或者是B+树这些数据结构实现功能,但这些复杂的数据结构都避免不了比较慢的随机读写操作,而我们希望随机读写能尽量减少,正是基于这个原理,LSMT被发明了出来。LSMT使用了一种独特的机制牺牲了一些读操作的性能,保证了写操作的能力,它能够让所有的操作顺序化,几乎完全避免了随机读写。
在我们介绍LSMT的原理之前,我们先来介绍一下它的子结构SSTable。
SSTable
次看到这个单词的时候觉得一头雾水是正常的,SSTable的全称是Sorted String Table,本质就是一个KV结构顺序排列的文件。我们来看下下图:

基础的SSTable就是上图当中右侧的部分,即key和value的键值对按照key值的大小排序,并存储在文件当中。当我们需要查找某个key值对应的数据的时候,我们会将整个文件读入进内存,进行查找。同样,写入也是如此,我们会将插入的操作在内存中进行,得到结果之后,直接覆盖原本的文件,而不会在文件当中修改,因为这会牵扯到移动大量的数据。
如果文件中的数据量过大,我们需要另外建立一个索引文件,存储不同的key值对应的offset,方便我们在读取文件的时候快速查找到我们想要查找的文件。索引文件即上图当中左边部分。
需要注意,SSTable是不可修改的,我们只会用新的SSTable去覆盖旧的,而不会再原本的基础上修改。因为修改会涉及随机读写,这是我们不希望的。
LSM的增删改查
理解了SSTable之后,我们来看下基本的LSM实现原理。
其实基本的LSM原理非常简单,本质上就是在SSTable的基础上增加了一个Memtable,Memtable顾名思义就是存放在内存当中的表结构。当然也不一定是表结构,也可以是树结构,这并不影响,总之是一个可以快速增删改查的数据结构,比如红黑树、SkipList都行。其次我们还需要一个log文件,和数据库当中的log一样,记录数据发生的变化。方便系统故障或者是数据丢失的时候进行找回,所以整体的架构如下:
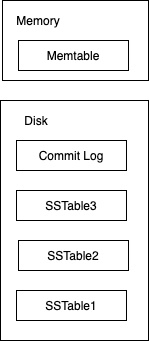
查找
我们先来看查找的情况,当我们需要查找一个元素的时候,我们会先查找Memtable。原因也很好理解,它就在内存当中,不需要额外读取文件,如果Memtable当中没有找到,我们再一个一个查找SSTable,由于SSTable当中的数据也是顺序存储的,所以我们可以使用二分查找,整个查找的速度也会非常快。
但是有一点,由于SSTable的数量可能会很多,而且我们必须要顺序查找,所以当SSTable数量很大的时候,也会影响查找的速度。为了解决这个问题,我们可以引入布隆过滤器进行优化。我们对每一个SSTable建立一个布隆过滤器,可以快速地判断元素是否在某一个SSTable当中。布隆过滤器判断元素不存在是一定准确的,而判断存在可能会有一个很小的几率失误,但这个失误率是可以控制的,我们可以设置合理的参数,使得失误率足够低。
加上了布隆过滤器之后的查找操作是这样的:

上图的星星表示布隆过滤器,也就是说我们先通过布隆过滤器判断元素是否存在之后,再进行查找。
布隆过滤器在之前的文章当中曾经和大家介绍过,有遗忘或者是新关注的同学可以点击下方链接回顾一下。
大数据算法——布隆过滤器
增删改
除了查找之外的其他操作都发生在Memtable当中,比如当我们要增加一个元素的时候,我们直接增加在Memtable,而不是写入文件。这也保证了增加的速度可以做到非常快。
除此之外,修改和删除也一样,如果需要修改的元素刚好在Memtable当中,没什么好说的我们直接进行修改。那如果不在Memtable当中,如果我们要先查找到再去修改免不了需要进行磁盘读写,这会消耗大量资源。所以我们还是在Memtable当中进行操作,我们会插入这个元素,标记成修改或者是删除。
所以我们可以把增删改这三个操作都看成是添加,但是这就带来了一个问题,这么操作会导致很快Memtable当中就积累了大量数据,而我们的内存资源也是有限的,显然不能无限拓张。为了解决这个问题,我们需要定期将Memtable当中的内容存储到磁盘,存储成一个SSTable。这也是SSTable的来源,SSTable当中的数据不是凭空出现的,而是LSM落盘产生的。
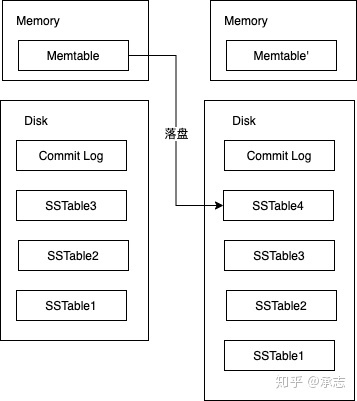
同样,由于我们不断地落盘同样也会导致SSTable的数量增加,前面我们也已经分析过了,SSTable的数量增加会影响我们查找的效率,所以我们不能放任它无限增加。再加上我们还存储了许多修改和删除的信息,我们需要把这些信息落实。为了达成这点,我们需要定期将所有的SSTable合并,在合并的过程当中我们完成数据的删除以及修改工作。换句话说,之前的删除、修改操作只是被记录了下来,直到合并的时候才真正执行。
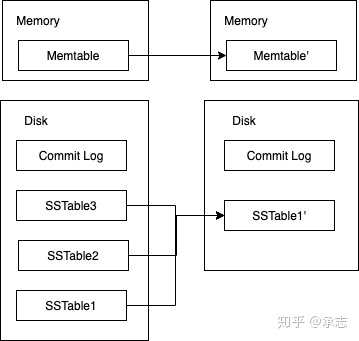
整个归并的过程并不难,类似于归并排序当中的归并操作,只是我们需要加上状态的判断。
总结
我们回顾一下LSMT的整个过程,虽然说是树,但其实树形结构并不明显。但如果我们观察一下查找元素时候的查询顺序,其实是从Memtable,然后沿着SSTable顺序往下的,这点和树形结构是一致的,可以看成一个比较”窄“的树。如果还是觉得这个数据结构长得不那么像一棵树是正常的,我们不用纠结。另外,从原理上来看,简直有些简单粗暴地过头,但是从实际结果来看,它的效果却非常好,在Hbase、kudu当中有着广泛应用。
我们对比一下它和B+树,在B+树当中,我们为了能够快速读取而使用了多路平衡树,这样可以迅速找到对应key的节点。我们只需要读入节点当中的内容即可,但也正因为平衡树的结构,导致了我们在写入数据的时候会引起树结构的变动,也就涉及到多次文件的随机读写。当我们数据的吞吐量很大的时候,会带来巨大的开销。而LSMT则不然,我们读取的时候效率比B+树要低,但是对于大数据的写入支持得更好。在大数据场景当中,许多对于数据的吞吐量有着很高的要求,比如消息系统、分布式存储等。这个时候B+树就有些无能为力了,但是同样,如果我们需要保证查找的效率,那LSMT也不太合适,因此两者其实并没有谁比谁更优,而是针对的场景不同。
后,关于LSMT,其实也有很多个变种,其中比较有名的是Jeff Dean写的Leveldb,它在LSMT的基础上做了一些改动,进一步提升了性能,相关的内容我们放到下篇文章。
今天的文章就是这些,如果觉得有所收获,请顺手点个关注或者转发吧,你们的举手之劳对我来说很重要。

