дёҖгҖҒеүҚиЁҖ
еҳҝпјҢе°ҸеӮ…е“ҘжҖҺд№ҲзӘҒ然讲еҲ°еӨ§е…¬зәҰж•°дәҶпјҹ
иҝҷд№ҲжғідҪ иӮҜе®ҡжҳҜжІЎжңүеҘҪеҘҪйҳ…иҜ»еүҚйқўз« иҠӮдёӯе°ҸеӮ…е“Ҙи®ІеҲ°зҡ„RSAз®—жі•пјҢеҜ№дәҺдёҺ欧жӢүз»“жһңи®Ўз®—зҡ„дә’дёәиҙЁж•°зҡ„е…¬й’ҘeпјҢе…¶е®һе°ұйңҖиҰҒдҪҝз”ЁеҲ°иҫ—иҪ¬зӣёйҷӨжі•жқҘи®Ўз®—еҮәеӨ§е…¬зәҰж•°гҖӮ
ж”ҫеҝғпјҢдҪ жүҖжңүеҶҷзҡ„д»Јз ҒпјҢйғҪжҳҜеҜ№ж•°еӯҰйҖ»иҫ‘зҡ„е…·дҪ“е®һзҺ°пјҢж— йқһжҳҜйҡҫжҳ“дёҚеҗҢзҪўдәҶгҖӮжүҖд»ҘеҰӮжһңдҪ зңҹзҡ„жғіеӯҰеҘҪзј–зЁӢжҖқз»ҙиҖҢдёҚеҸӘжҳҜCRUDпјҢйӮЈе°ұиҰҒжҠҠж•°жҚ®з»“жһ„гҖҒз®—жі•йҖ»иҫ‘зӯүж №еҹәжү“зүўгҖӮ
дәҢгҖҒзҹӯйҷӨжі•
既然йғҪиҜҙеҲ°иҝҷдәҶпјҢйӮЈдҪ иҝҳи®°еҫ—жҖҺд№Ҳи®Ўз®—еӨ§е…¬зәҰж•°еҗ—пјҢжӯ»й¬јпјҹ

д»ҘдёҠиҝҷз§Қж–№ејҸе°ұжҳҜжҲ‘们еңЁдёҠеӯҰйҳ¶ж®өеӯҰд№ зҡ„пјҢиҝҷз§Қи®Ўз®—ж–№ејҸеҸ«еҒҡзҹӯйҷӨжі•гҖӮ
зҹӯйҷӨжі•пјҡжҳҜз®—жңҜдёӯйҷӨжі•зҡ„з®—жі•пјҢе°ҶйҷӨжі•иҪ¬жҚўжҲҗдёҖиҝһдёІзҡ„иҝҗз®—гҖӮзҹӯйҷӨжі•жҳҜз”ұй•ҝйҷӨжі•з®ҖеҢ–иҖҢжқҘпјҢеҪ“дёӯдјҡз”ЁеҲ°еҝғз®—пјҢеӣ жӯӨйҷӨж•°иҫғе°Ҹзҡ„йҷӨжі•жҜ”иҫғйҖӮз”ЁзҹӯйҷӨжі•гҖӮеҜ№еӨ§йғЁеҲҶзҡ„дәәиҖҢиЁҖпјҢиӢҘйҷӨд»Ҙ12жҲ–12д»ҘдёӢзҡ„ж•°пјҢеҸҜд»Ҙз”Ёи®°еҝҶдёӯд№ҳжі•иЎЁзҡ„еҶ…е®№пјҢз”Ёеҝғз®—жқҘиҝӣиЎҢзҹӯйҷӨжі•гҖӮд№ҹжңүдәӣдәәеҸҜд»ҘеӨ„зҗҶйҷӨж•°жӣҙеӨ§зҡ„зҹӯйҷӨжі•гҖӮвҖ”вҖ” жқҘиҮӘз»ҙеҹәзҷҫ科
дёүгҖҒ欧еҮ йҮҢеҫ·з®—жі•
зҹӯйҷӨжі•иғҪи§ЈеҶіи®Ўз®—еӨ§е…¬зәҰж•°зҡ„й—®йўҳпјҢдҪҶж”ҫеҲ°зЁӢеәҸзј–еҶҷдёӯжҖ»жҳҜеҫҲеҲ«жүӯпјҢжҖ»дёҚиғҪдёҖдёӘдёӘж•°еӯ—еҺ»иҜ•з®—пјҢиҝҷе°ұжҳҫеҫ—еҫҲй—№жҢәгҖӮе…¶е®һйҷӨдәҶзҹӯйҷӨжі•иҝҳжңүдёҖз§ҚжҳҜи®Ўз®—е…¬зәҰж•°зҡ„еҠһжі•пјҢеҸ«еҒҡ欧еҮ йҮҢеҫ·з®—жі•гҖӮ
欧еҮ йҮҢеҫ·з®—жі•пјҡжҳҜи®Ўз®—дёӨдёӘж•ҙж•°пјҲж•°еӯ—пјүзҡ„еӨ§е…¬зәҰж•°гҖҗGCD(Greatest Common Divisor)гҖ‘зҡ„жңүж•Ҳж–№жі•пјҢеҚіиғҪе°Ҷе®ғ们ж•ҙйҷӨиҖҢж— дҪҷж•°зҡ„еӨ§ж•°гҖӮе®ғд»ҘеҸӨеёҢи…Ҡж•°еӯҰ家 欧еҮ йҮҢеҫ—зҡ„еҗҚеӯ—е‘ҪеҗҚпјҢ欧еҮ йҮҢеҫ·еңЁд»–зҡ„еҮ дҪ•еҺҹжң¬пјҲзәҰе…¬е…ғеүҚ 300 е№ҙпјүдёӯжҸҸиҝ°дәҶе®ғгҖӮе®ғжҳҜз®—жі•зҡ„зӨәдҫӢпјҢжҳҜж №жҚ®жҳҺзЎ®е®ҡд№үзҡ„规еҲҷжү§иЎҢи®Ўз®—зҡ„еҲҶжӯҘиҝҮзЁӢпјҢ并且жҳҜеёёз”Ёзҡ„еҸӨиҖҒзҡ„з®—жі•д№ӢдёҖгҖӮе®ғеҸҜд»Ҙз”ЁжқҘеҮҸе°‘еҲҶж•°еҲ°д»–们зҡ„з®ҖеҚ•зҡ„еҪўејҸпјҢ并且жҳҜи®ёеӨҡе…¶д»–ж•°и®әе’ҢеҜҶз Ғи®Ўз®—зҡ„дёҖйғЁеҲҶгҖӮвҖ”вҖ” жқҘиҮӘз»ҙеҹәзҷҫ科
GCDпјҢд»ЈиЎЁдәҶдёӨдёӘж•°еӯ—зҡ„еӨ§е…¬зәҰж•°пјҢGCD(X,Y) = ZпјҢйӮЈд№Ҳе°ұиЎЁзӨә X е’Ң Y зҡ„еӨ§е…¬зәҰж•°жҳҜ ZгҖӮз”ұ欧еҮ йҮҢеҫ·з®—жі•з»ҷеҮә GCD(X,Y) = GCD(Y,XmodY) вҖ”вҖ” mod иЎЁзӨәжұӮжЁЎи®Ўз®—дҪҷж•°гҖӮ
е…¶е®һз®ҖеҚ•жқҘиҜҙе°ұжҳҜпјҢXе’ҢYзҡ„е…¬зәҰж•°жҳҜZпјҢйӮЈд№ҲYе’ҢZзҡ„е…¬зәҰж•°д№ҹжҳҜZгҖӮ24е’Ң18зҡ„еӨ§е…¬зәҰж•°жҳҜ6пјҢйӮЈд№Ҳ18е’Ң6зҡ„е…¬зәҰж•°д№ҹжҳҜ6гҖӮеҳҝпјҢе°ұиҝҷд№ҲдёҖдёӘдәӢгҖӮдҪҶе°ұеӣ дёәжңүдәҶиҝҷдёҖж ·дёҖжқЎжҺЁи®әпјҢи®©зј–зЁӢд»Јз ҒеҸҳеҫ—дјҳйӣ…иҲ’жңҚпјҢеҸӘйңҖиҰҒдёҚж–ӯең°е°ҶXгҖҒYдёӨж•°дҪңе·®пјҢе°ұиғҪи®Ўз®—еӨ§е…¬зәҰж•°гҖӮ
рҹҳӮ иҝҷи®©е°ҸеӮ…е“Ҙжғіиө·пјҢеӨҡе№ҙеүҚдёҠеӯҰж—¶еҖҷпјҢжҲ‘д№ҹз»ҷеҮәиҝҮдёҖжқЎжҺЁи®әпјӣвҖқд»»ж„ҸдёҖз»„жүҖиғҪжһ„жҲҗзӯүе·®ж•°еҲ—зҡ„дёүдёӘж•°еӯ—пјҢжүҖиғҪз»„еҗҲеҮәжқҘзҡ„дёҖдёӘдёүдҪҚж•°пјҢйғҪиғҪиў«3ж•ҙйҷӨгҖӮвҖң дҫӢеҰӮпјҡзӯүе·®ж•°еҲ— 16гҖҒ31гҖҒ46 з»„еҗҲжҲҗдёүдҪҚж•° 463116 жҲ–иҖ… 461631 йғҪиғҪиў«3ж•ҙйҷӨгҖӮ
еӣӣгҖҒиҫ—иҪ¬зӣёйҷӨжі•д»Јз Ғе®һзҺ°
欧еҮ йҮҢеҫ·з®—жі• = иҫ—иҪ¬зӣёйҷӨжі•жі•пјҡhttps://en.wikipedia.org/wiki/Euclidean_algorithm
еңЁиҫ—иҪ¬зӣёйҷӨжі•зҡ„е®һзҺ°дёӯпјҢи®Ўз®—еӨ§е…¬зәҰж•°зҡ„ж–№ејҸпјҢе°ұжҳҜдҪҝз”ЁдёҖдёӘж•°еӯ—еҮҸеҺ»еҸҰеӨ–дёҖдёӘж•°еӯ—пјҢзӣҙеҲ°дёӨдёӘж•°еӯ—зӣёеҗҢжҲ–иҖ…жңүе…¶дёӯдёҖдёӘж•°еӯ—дёә0пјҢйӮЈд№ҲеҗҺдёҚдёәйӣ¶зҡ„йӮЈдёӘж•°еӯ—е°ұжҳҜдёӨж•°зҡ„еӨ§е…¬зәҰж•°гҖӮ
е°ҸеӮ…е“ҘеңЁиҝҷйҮҢжҸҗдҫӣдәҶ2з§Қи®Ўз®—ж–№ејҸпјҢдёҖз§ҚжҳҜеҫӘзҺҜеҸҰеӨ–дёҖз§ҚжҳҜйҖ’еҪ’гҖӮвҖ”вҖ” ж–№дҫҝеҫҲеӨҡзңӢдёҚжҮӮйҖ’еҪ’зҡ„е°ҸдјҷдјҙеҸҜд»Ҙз”ЁеҸҰеӨ–зҡ„ж–№ејҸеӯҰд№ гҖӮ
1. еҫӘзҺҜе®һзҺ°
public long gcd01(long m, long n) {
m = Math.abs(m);
n = Math.abs(n);
while (m != && n != && m != n) {
if (m > n) {
m = m - n;
} else {
n = n - m;
}
}
return m == ? n : m;
}
- дёӨж•°еҫӘзҺҜеӨ„зҗҶдёӯпјҢжқЎд»¶дёә
m != 0 && n != 0 && m != nзӣҙиҮіеҫӘзҺҜз»“жқҹгҖӮ
2. йҖ’еҪ’е®һзҺ°
public long gcd02(long m, long n) {
if (m < n) {
long k = m;
m = n;
n = k;
}
if (m % n != ) {
long temp = m % n;
return gcd02(n, temp);
} else {
return n;
}
}
- и®Ўз®—ж–№ејҸйҖ»иҫ‘е’ҢжқЎд»¶жҳҜдёҖж ·зҡ„пјҢеҸӘдёҚиҝҮиҝҷдёӘжҳҜдҪҝз”ЁдәҶйҖ’еҪ’и°ғз”Ёзҡ„ж–№ејҸиҝӣиЎҢеӨ„зҗҶгҖӮ
3. жөӢиҜ•йӘҢиҜҒ
@Test
public void test_euclidean() {
Euclidean euclidean = new Euclidean();
System.out.println(euclidean.gcd01(124, 20));
System.out.println(euclidean.gcd02(124, 20));
}
жөӢиҜ•з»“жһң
4
4
Process finished with exit code
- и®Ўз®— 124 е’Ң 20 зҡ„еӨ§е…¬зәҰж•°пјҢдёӨдёӘи®Ўз®—ж–№ејҸз»“жһңйғҪжҳҜ 4 гҖӮеҘҪзҡ„пјҢеҲ°иҝҷжөӢиҜ•йҖҡиҝҮгҖӮ
- иҝҷ并дёҚжҳҜдёҖдёӘеҫҲйҡҫзҡ„зҹҘиҜҶзӮ№пјҢдҪҶеҪ“дҪ еҒҡдёҖдәӣжҠҖжңҜеҲҶдә«гҖҒзӯ”иҫ©иҝ°иҒҢзӯүж—¶еҖҷпјҢиғҪиҝҷж ·з”ЁжҠҖжңҜиҜӯиЁҖиҖҢдёҚжҳҜеӨ§зҷҪиҜқзҡ„и®Іиҝ°еҮәжқҘеҗҺпјҢе…¶е®һй«ҳеәҰе°ұжңүдәҶгҖӮе…„ејҹпјҒрҹ‘¬рҹҸ»
еңЁ stackoverflow.com зңӢеҲ°дёҖйҒ“й—®йўҳпјҡи®Ўз®—дёӨдёӘж•ҙж•°зҡ„е°Ҹе…¬еҖҚж•°зҡ„жңүж•Ҳж–№жі•жҳҜд»Җд№Ҳпјҹ

д№ҚдёҖзңӢпјҢрҹӨЁ иҝҷиғҪжңүе•ҘгҖӮдёҚе°ұжҳҜи®Ўз®—дёӢе°Ҹе…¬еҖҚж•°еҗ—пјҹдҪҶдёҖжғіжҲ‘и„‘иўӢдёӯи®Ўз®—е°Ҹе…¬еҖҚж•°зҡ„ж–№жі•пјӣдёҖз§ҚжҳҜеңЁжң¬еӯҗдёҠйҖҡиҝҮзҹӯйҷӨжі•и®Ўз®—пјҢеҸҰеӨ–дёҖз§ҚжҳҜеҹәдәҺи®Ўз®—еҮәзҡ„еӨ§е…¬зәҰж•°пјҢеҶҚдҪҝз”Ёе…¬ејҸпјҡlcm(a, b) = |a * b| / gcd(a, b) жұӮеҫ—е°Ҹе…¬еҖҚж•°гҖӮвҖ”вҖ” и®Ўз®—еӨ§е…¬зәҰж•°жҳҜеҹәдәҺ欧еҮ йҮҢеҫ·з®—жі•(иҫ—иҪ¬зӣёйҷӨжі•)
йӮЈд№Ҳиҝҷж ·зҡ„и®Ўз®—ж–№жі•жҳҜдёҚжҳҜжңүж•Ҳзҡ„ж–№жі•пјҢеҸҰеӨ–еҰӮжһңжҳҜеҗҢж—¶и®Ўз®—еӨҡдёӘж•ҙж•°зҡ„е°Ҹе…¬еҖҚж•°пјҢиҰҒжҖҺд№ҲеӨ„зҗҶпјҹ
е…¶е®һзј–зЁӢзҡ„еӯҰд№ еҫҖеҫҖе°ұжҳҜиҝҷж ·пјҢз•ҷеҝғеӨ„еӨ„йғҪжҳҜеӯҰй—®пјҢдҪ жҖ»жҳҜйңҖиҰҒд»Һеҗ„з§Қз»Ҷе°Ҹзҡ„зӮ№дёӯпјҢз§ҜзҙҜиҮӘе·ұзҡ„жҠҖжңҜжҖқз»ҙе№ҝеәҰе’Ңзәөеҗ‘жҺўзҙўж·ұеәҰгҖӮеҘҪе•ҰпјҢжҺҘдёӢжқҘе°ҸеӮ…е“Ҙе°ұз»ҷеӨ§е®¶д»Ӣз»ҚеҮ з§Қз”ЁдәҺи®Ўз®—е°Ҹе…¬еҖҚж•°зҡ„з®—жі•гҖӮ
дә”гҖҒз”Ёе…¬зәҰж•°е®һзҺ°
е…¬ејҸпјҡlcm(a, b) = |a * b| / gcd(a, b)
public long lcm01(long m, long n) {
return ((m == ) || (n == )) ? : Math.abs(m * n) / gcd(m, n);
}
private long gcd(long m, long n) {
m = Math.abs(m);
n = Math.abs(n);
// д»ҺдёҖдёӘж•°еӯ—дёӯеҮҸеҺ»еҸҰдёҖдёӘж•°еӯ—пјҢзӣҙеҲ°дёӨдёӘж•°еӯ—еҸҳеҫ—зӣёеҗҢгҖӮ
// иҝҷе°ҶжҳҜ GCDгҖӮеҰӮжһңе…¶дёӯдёҖдёӘж•°еӯ—дёәйӣ¶пјҢд№ҹйҖҖеҮәеҫӘзҺҜгҖӮ
// https://en.wikipedia.org/wiki/Euclidean_algorithm
while (m != && n != && m != n) {
if (m > n) {
m = m - n;
} else {
n = n - m;
}
}
return m == ? n : m;
}
- йҰ–е…ҲиҝҷйҮҢжҳҜдёҖдёӘжҜ”иҫғз®ҖеҚ•зҡ„ж–№ејҸпјҢеҹәдәҺдёӨж•°д№ҳз§ҜйҷӨд»ҘеӨ§е…¬зәҰж•°пјҢеҫ—еҲ°зҡ„з»“жһңе°ұжҳҜе°Ҹе…¬еҖҚж•°гҖӮ
е…ӯгҖҒз®ҖеҚ•зҙҜеҠ и®Ўз®—
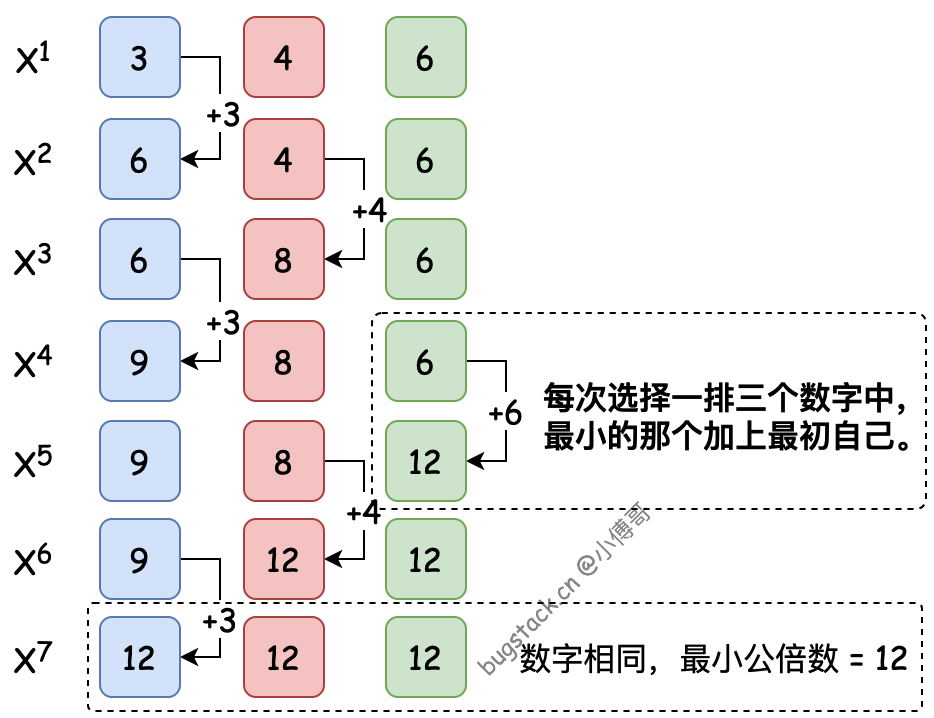
жӯӨи®Ўз®—ж–№ејҸдёәпјҢеңЁдёҖз»„жӯЈж•ҙж•°ж•°еҲ—дёӯпјҢйҖҡиҝҮжүҫеҲ°е°Ҹзҡ„ж•°еӯ—иҝӣиЎҢиҮӘиә«зҙҜеҠ еҫӘзҺҜпјҢзӣҙиҮіжүҖжңүж•°еӯ—зӣёеҗҢж—¶пјҢеҲҷиҝҷдёӘж•°еӯ—дёәе°Ҹе…¬еҖҚж•°гҖӮвҖ”вҖ” дҪ иғҪд»Јз Ғе®һзҺ°дёҖдёӢеҗ—пјҹ
public long lcm02(long... n) {
long[] cache = n.clone();
// д»ҘжүҖжңүж•°еӯ—йғҪзӣёзӯүдҪңдёәжқЎд»¶
while (!isEquals(n)) {
System.out.println(JSON.toJSONString(n));
long min = n[];
int idx = ;
for (int i = ; i < n.length; i++) {
if (min > n[i]) {
min = n[i];
idx = i;
}
}
n[idx] = cache[idx] + min;
}
return n[];
}
- еңЁд»Јз Ғе®һзҺ°дёӯпјҢйҰ–е…ҲиҰҒжҠҠnдёӘж•ҙж•°ж•°еҲ—иҝӣиЎҢе…ӢйҡҶдҝқеӯҳгҖӮеӣ дёәжҜҸж¬ЎзӣёеҠ зҡ„йғҪжҳҜеҲқзҡ„иҝҷдёӘж•°еҲ—йҮҢзҡ„ж•°еӯ—еҖјгҖӮжҺҘдёӢжқҘе°ұжҳҜд»ҘжүҖжңүж•°еӯ—йғҪзӣёзӯүдҪңдёәжқЎд»¶еҫӘзҺҜеҲӨж–ӯпјҢдёҚж–ӯең°зҡ„зҙҜеҠ е°Ҹзҡ„ж•°еҖјеҚіеҸҜгҖӮз»Ҳиҝ”еӣһзҡ„е°ұжҳҜе°Ҹе…¬еҖҚж•°гҖӮ
дёғгҖҒиЎЁж јжҺЁжј”и®Ўз®—
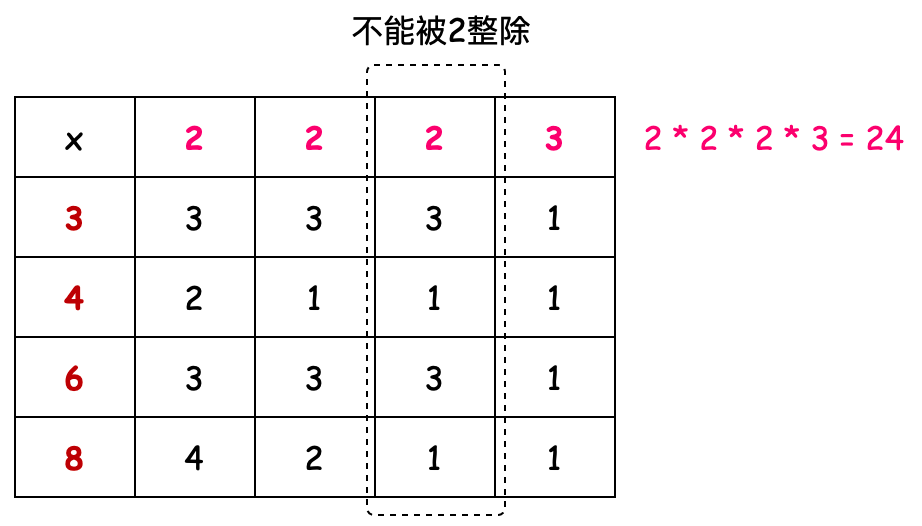
иЎЁж ји®Ўз®—ж–№ејҸдёәе°ҶдёҖз»„ж•°еӯ—д»Ҙе°Ҹзҡ„иҙЁж•°2ејҖе§Ӣж•ҙйҷӨпјҢзӣҙеҲ°дёҚиғҪиў«2ж•ҙйҷӨеҗҺпјҢз”ЁдёӢдёҖдёӘиҙЁж•°3继з»ӯж•ҙйҷӨпјҲеү©дҪҷзҡ„ж•°еӯ—дёӯжҜ”еӨ§зҡ„е°Ҹзҡ„иҙЁж•°пјүзӣҙиҮіжүҖжңүж•°еӯ—йғҪдёә1зҡ„ж—¶еҖҷз»“жқҹгҖӮз»ҲжүҖжңүжңүж•Ҳзҡ„иҙЁж•°д№ҳз§Ҝе°ұжҳҜе°Ҹе…¬еҖҚж•°гҖӮвҖ”вҖ” жғіжғіеҰӮжһңиҝҷи®©дҪ з”Ёд»Јз Ғе®һзҺ°пјҢдҪ иғҪиӮқеҮәжқҘеҗ—пјҹ
public long lcm03(long... n) {
Map<Long, List<Long>> keys = new HashMap<>();
for (long key : n) {
keys.put(key, new ArrayList<Long>() {{
add(key);
}});
}
System.out.print("жү§иЎҢиЎЁж ји®Ўз®—пјҡ\r\nx ");
long primality = 2, cachePrimality = primality, filterCount = , lcm = 1;
// д»ҘжүҖжңүе…ғзҙ еҗҺдёҖдҪҚдёә1дҪңдёәжқЎд»¶
while (filterCount != keys.size()) {
int refresh = ;
filterCount = ;
for (Map.Entry<Long, List<Long>> entry : keys.entrySet()) {
long value = entry.getValue().get(entry.getValue().size() - 1);
if (value == 1) {
filterCount++;
}
// ж•ҙйҷӨеӨ„зҗҶ
if (value % primality == ) {
entry.getValue().add(value / primality);
refresh++;
} else {
entry.getValue().add(value);
}
}
// еҲ·ж–°йҷӨж•°
if (refresh == ) {
for (Map.Entry<Long, List<Long>> entry : keys.entrySet()) {
long value = entry.getValue().get(entry.getValue().size() - 1);
// жүҫеҲ°дёӢдёҖдёӘз¬ҰеҗҲзҡ„зҙ ж•°
if (value > primality || (value < cachePrimality && value > primality)) {
cachePrimality = value;
}
entry.getValue().remove(entry.getValue().size() - 1);
}
primality = cachePrimality;
} else {
// зҙҜи®Ўд№ҳз§Ҝ
lcm *= cachePrimality;
System.out.print(cachePrimality + " ");
}
}
keys.forEach((key, values) -> {
System.out.println();
for (long v : values) {
System.out.print(v + " ");
}
});
System.out.println("\r\n");
return lcm;
}
- еңЁд»Јз Ғе®һзҺ°дёӯжҲ‘们йҖҡиҝҮ Map дҪңдёәиЎЁзҡ„keyпјҢMap дёӯзҡ„ List дҪңдёәиЎЁжҜҸдёҖиЎҢж•°жҚ®гҖӮйҖҡиҝҮиҝҷж ·дёҖдёӘз»“жһ„жһ„е»әеҮәдёҖеј иЎЁгҖӮ
- жҺҘдёӢжқҘд»ҘжүҖжңүе…ғзҙ еҗҺдёҖдҪҚдёә1дҪңдёәжқЎд»¶еҫӘзҺҜеӨ„зҗҶж•°жҚ®пјҢз”ЁејҖе§Ӣзҡ„2дҪңдёәзҙ ж•°ж•ҙйҷӨеҲ—иЎЁдёӯзҡ„ж•°жҚ®пјҢ并дҝқеӯҳеҲ°дёӢдёҖз»„ж•°еҲ—дёӯгҖӮеҪ“2дёҚиғҪж•ҙйҷӨж—¶пјҢеҲҷеҲ·ж–°зҙ ж•°пјҢйҖүеҸ–еҸҰеӨ–дёҖдёӘеҲ—иЎЁдёӯе°Ҹзҡ„зҙ ж•°дҪңдёәйҷӨ数继з»ӯгҖӮ
- иҝҷдёӘиҝҮзЁӢдёӯдјҡзҙҜи®Ўжңүж•Ҳзҙ ж•°зҡ„д№ҳз§ҜпјҢиҝҷдёӘд№ҳз§Ҝзҡ„з»Ҳз»“жһңе°ұжҳҜе°Ҹе…¬еҖҚж•°гҖӮ
е…«гҖҒжөӢиҜ•йӘҢиҜҒ
еҚ•е…ғжөӢиҜ•
@Test
public void test_euclidean() {
LastCommonMultiple lastCommonMultiple = new LastCommonMultiple();
// System.out.println("е°Ҹе…¬еҖҚж•°пјҡ" + lastCommonMultiple.lcm01(2, 7));
System.out.println("е°Ҹе…¬еҖҚж•°пјҡ" + lastCommonMultiple.lcm02(3, 4, 6));
// System.out.println("е°Ҹе…¬еҖҚж•°пјҡ" + lastCommonMultiple.lcm03(3, 4, 6));
System.out.println("е°Ҹе…¬еҖҚж•°пјҡ" + lastCommonMultiple.lcm03(3, 4, 6, 8));
//System.out.println("е°Ҹе…¬еҖҚж•°пјҡ" + lastCommonMultiple.lcm03(4, 7, 12, 21, 42));
}
жөӢиҜ•з»“жһң
жү§иЎҢзҙҜеҠ и®Ўз®—пјҡ
[3,4,6]
[6,4,6]
[6,8,6]
[9,8,6]
[9,8,12]
[9,12,12]
е°Ҹе…¬еҖҚж•°пјҡ12
жү§иЎҢиЎЁж ји®Ўз®—пјҡ
x 2 2 2 3
3 3 3 3 1
4 2 1 1 1
6 3 3 3 1
8 4 2 1 1
е°Ҹе…¬еҖҚж•°пјҡ24
- еҲ°иҝҷйҮҢжөӢиҜ•е°ұз»“жқҹдәҶпјҢжң¬з« дёҖе…ұд»Ӣз»ҚдәҶдёүз§Қи®Ўз®—е°Ҹе…¬еҖҚж•°зҡ„ж–№жі•гҖӮйӮЈеҰӮжһңеҸӘи®©дҪ зңӢеҲ°йҖ»иҫ‘пјҢдҪ иғҪеҶҷеҮәз»Ҳзҡ„д»Јз Ғеҗ—пјҹ
д№қгҖҒеёёи§ҒйқўиҜ•
- еӨ§е…¬зәҰж•°зҡ„дҪҝз”Ёз”ЁйҖ”пјҹ
- еҰӮдҪ•дҪҝз”Ёд»Јз Ғе®һзҺ°еӨ§е…¬зәҰж•°и®Ўз®—пјҹ
- дҪ жҳҜеҗҰдәҶ解欧еҮ йҮҢеҫ·з®—жі•пјҹ
- е…ідәҺж•°и®әдҪ иҝҳи®°еҫ—еӨҡе°‘пјҹ
- RSA еҠ еҜҶз®—жі•дёәд»Җд№ҲйңҖиҰҒз”ЁеҲ°е…¬зәҰж•°и®Ўз®—пјҹ
- еҰӮдҪ•и®Ўз®—дёӨж•°зҡ„е°Ҹе…¬еҖҚж•°пјҹ
- еҰӮжһңи®Ўз®—еӨҡдёӘж•ҙж•°зҡ„е°Ҹе…¬еҖҚж•°пјҹ
- дҪ иғҪиҜҙдёҖдёӢе…·дҪ“еҰӮдҪ•е®һзҺ°иҝҷз§ҚXзҡ„и®Ўз®—жөҒзЁӢеҗ—пјҹ
- дҪ зҹҘйҒ“е°Ҹе…¬еҖҚж•°и®Ўз®—зҡ„з”ЁйҖ”еҗ—пјҹ
- What is the most efficient way to calculate the least common multiple of two integers?пјҡhttps://stackoverflow.com/questions/3154454/what-is-the-most-efficient-way-to-calculate-the-least-common-multiple-of-two-int/3154503#3154503
- Least common multipleпјҡhttps://en.wikipedia.org/wiki/Least_common_multiple
- Chebyshev functionпјҡhttps://en.wikipedia.org/wiki/Chebyshev_function
- 欧еҮ йҮҢеҫ·з®—жі•пјҡhttps://en.wikipedia.org/wiki/Euclidean_algorithm
- зәҝжҖ§з»„еҗҲпјҡhttps://en.wikipedia.org/wiki/Linear_combination
- иҙқзҘ–е®ҡзҗҶпјҡhttps://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity
