二叉堆

二叉堆是一颗完全二叉树，该树中的某个节点的值总是不大于(不小于)其左右子节点的值，包括小堆和大堆。可以通过下图理解，为什么会使用数组来保存呢？因为利用完全二叉树的性质，我们可以通过数组来表示完全二叉树(数组下标与完全二叉树节点存在映射关系，比如父节点可以通过Math.floor((index-1)/2)来获取、左子节点可以通过2index+1来获取、右子节点可以通过2index+2来获取，从而简化了实现及开销，避免使用额外的指针来实现树结构。

小(大)堆性质

• 树根节点的值是所有堆节点值中小(大)值。

• 树中每个节点的子树也都是小(大)堆。

小(大)堆作用

小(大)堆能保证堆顶元素为小，而如果使用数组无法达到该效果。数组如果要访问小值则需要遍历查找小值，时间复杂度至少O(n)。而小堆访问小值时间复杂度为O(1)，当然天底下没有免费的午餐，我们需要做额外的工作去维护小(大)堆的结构，这也是需要复杂度花销的。

当然这也是小(大)堆的优势，通过动态维护使得小值的获取代价很小，实际上维护的时间复杂度为O(logN)。而数组则无法做到如此，如果数组想要维护顺序性则需要的复杂度至少为O(N)。这样来看小(大)堆的优势就凸现出来了。

插入操作

为避免冗长累赘，我们这里只挑小堆作为例子进行说明，大堆的情况与大堆相似。

现在分别插入4 7 2 5 6 1 0 3 8，使用一个数组来保存小堆。为了帮助理解，数组下方提供一个逻辑上的完全二叉树的结构，两者结合着更容易理解其中机制。首先插入4。

接着插入7，插入后检测到树符合小堆要求，所以不改动。

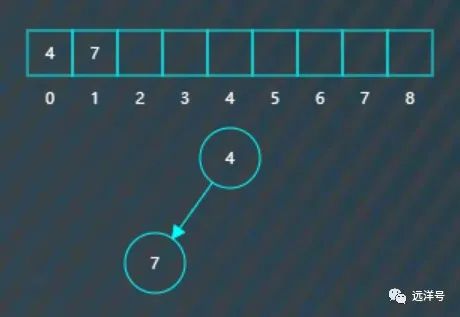
继续插入2，插入后检测到不符合小堆要求，父节点4大于右子节点2。

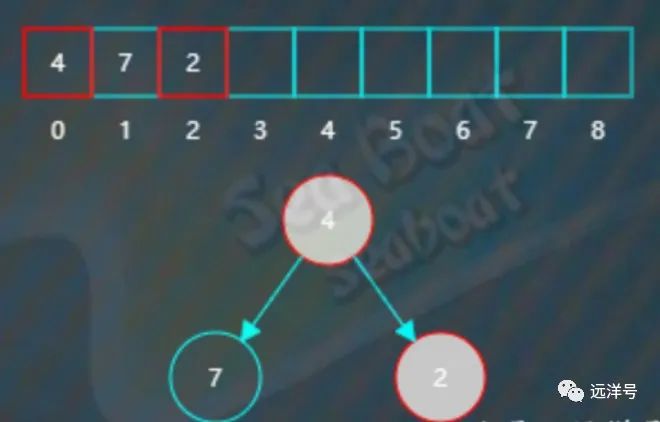
于是将它们对调。

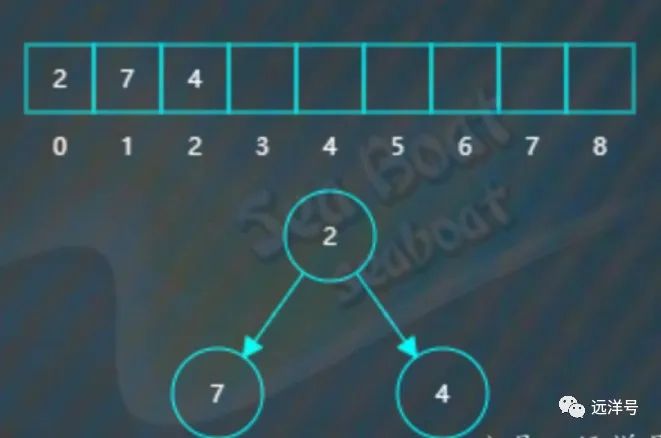
继续插入5，插入后检测到不符合小堆要求，父节点7大于左子节点5。

于是将它们对调。

继续插入6，插入后检测到树符合小堆要求，所以不改动。

继续插入1，插入后检测到不符合小堆要求，父节点4大于左子节点1。

于是将它们对调。

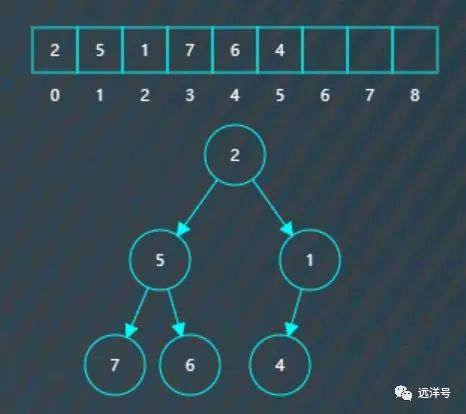
对调后继续检测到不符合小堆要求，父节点2大于右子节点1。

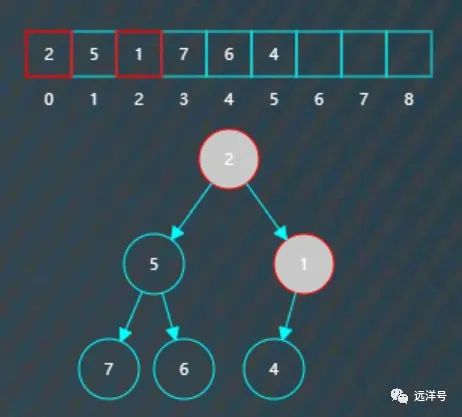
继续将它们对调。

继续插入0，插入后检测到不符合小堆要求，父节点2大于右子节点0。

于是将它们对调。

对调后继续检测到不符合小堆要求，父节点1大于右子节点0。

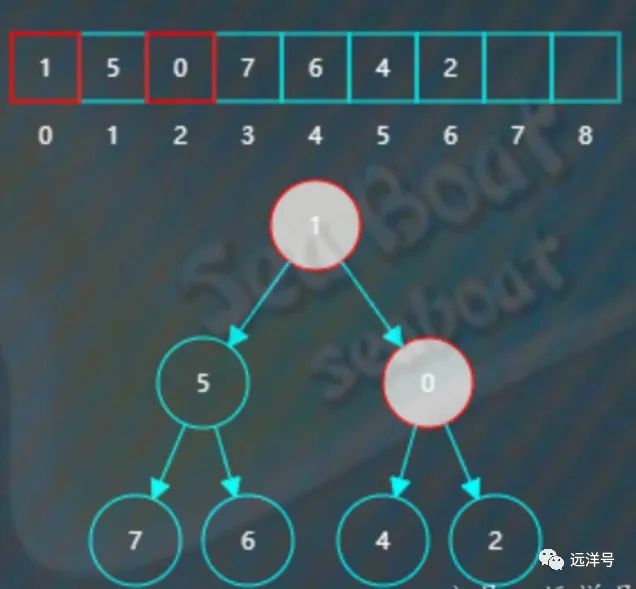
继续将它们对调。

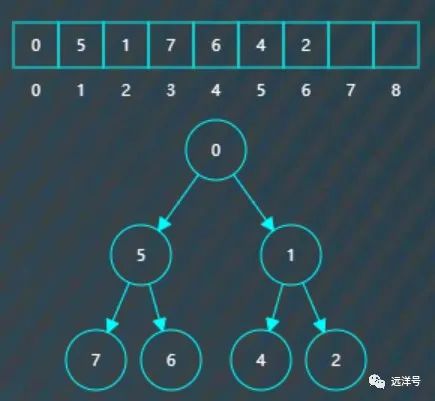
继续插入3，插入后检测到不符合小堆要求，父节点7大于左子节点3。

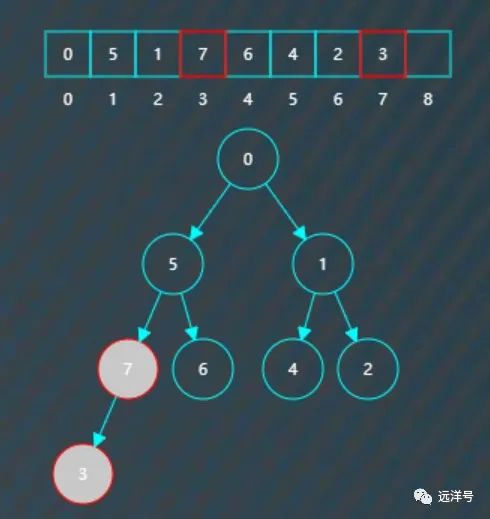
于是将它们对调。

对调后继续检测到不符合小堆要求，父节点5大于左子节点3。

继续将它们对调，然后符合小堆要求，不必继续往上对调。

继续插入8，插入后检测到树符合小堆要求，所以不改动。以上，完成所有元素的小堆插入操作。

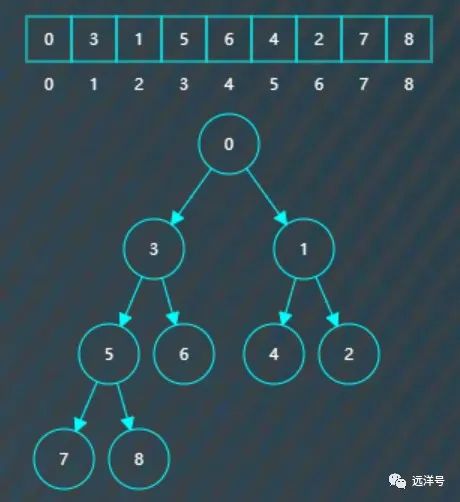
删除操作

删除操作其实就是删除小值，即小堆树中的根节点。主要是将树中后一个节点替换到被删除的根节点，然后自顶向下递归调整使之符合小堆要求。

删除根节点0，然后将树的后一个节点8补到根节点上。

比较根节点的左右子节点。

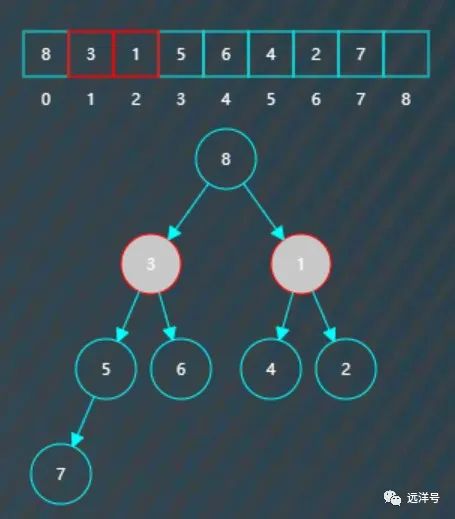
因为右子节点1比较小，所以我们要进一步比较的是根节点8与右子节点1。

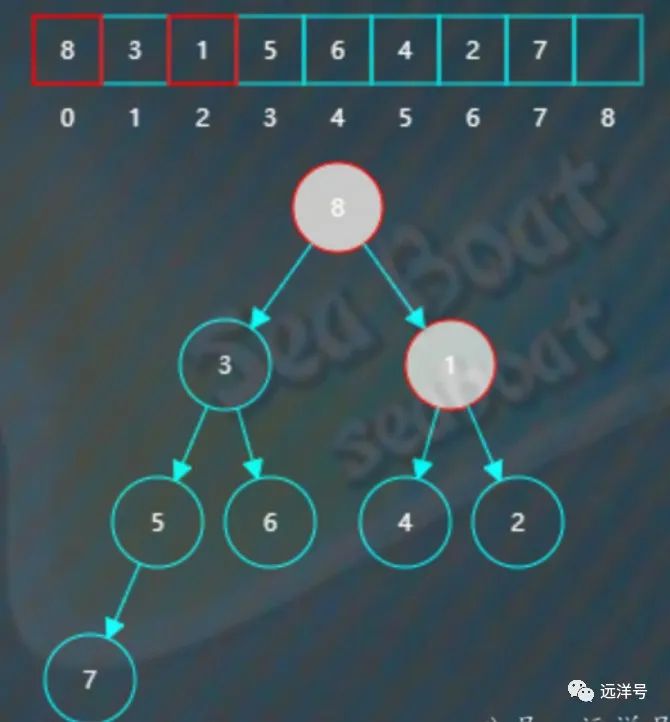
1小于8，于是对调。

继续比较现在节点8的左右子节点。

因为右子节点2比较小，所以我们要进一步比较的是根节点8与右子节点2。

2小于8，于是对调。

至此，完成小值删除操作。