首先,在正确时间顺序下,Optiver数据应该如下所示:
图1:在正确时间顺序下的,Optiver数据样例[1]
而量化里,数据时效性很高,很多时候预测,更多依赖于近期的行情表现,那如果知道目标时间点周围时间点的target,很可能会降低我们预测的不确定性。那在Optiver时间特征time_id不能真实反映时间顺序的情况下,我们可以依赖其他特征找到近邻样本,而不是依赖time_id来找近邻样本。在找到近邻样本后,我们对近邻样本的target值做聚合统计特征,加入模型训练即可。示意图如下:
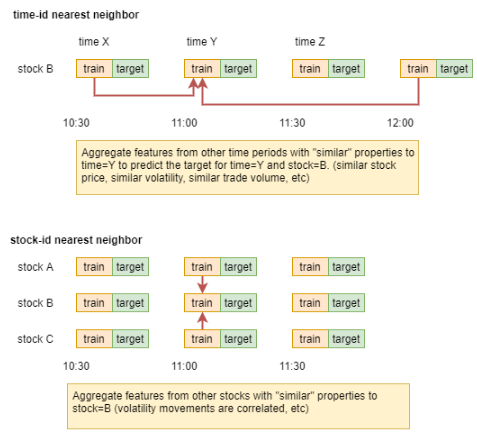
图2:时间和股票的近邻示意图[1]
如图2所示,不仅可以找出时间近邻样本,还能找到股票近邻样本。具体的实现步骤如下:
1. 基于重要特征f,在times/stocks上,找近邻样本;
2. 对近邻样本的目标变量target做聚合特征。
在这个过程中,你可以自主配置相关参数:
● 近邻的距离度量方式:曼哈顿距离、欧式距离等;
● 近邻样本聚合长度;3、20、30等;
● 近邻样本聚合统计方式:mean、min、max、std等;
但直接拿Optiver开源代码[2]会有两点问题:
1. 它直接在全数据集上做近邻搜索,忽略的时间先后顺序,而在真实场景下,time_id一般是有序,直接应用他开源代码在真实场景下,会有时间穿越的风险;
2. 在真实场景时,我们不可能在横截面上找近邻stock做聚类target特征,因为你不可能知道预测当天,其它stocks的target表现。
因此,我基于Kaggle:Ubiquant Market Prediction的数据集(time_id是真实有序的,且同time_id下stock们的target是不可见的),代码改进,使得每次近邻的搜索空间都在历史时间点内,同时只做time-along的近邻搜索,而不做stock-along的近邻搜索。
Ubiquant的数据样例如下:

数据说明:
● investment_id: A股资产id;
● time_id:有序的时间id;
● f0-f299:300个匿名特征;
● target:横截面标准化后的收益率。
我们先定义求近邻样本的聚合特征的函数:
from tqdm import tqdmimport copyimport pandas as pdimport numpy as npfrom sklearn.preprocessing import minmax_scalefrom sklearn.neighbors import NearestNeighborsdef make_nn_feature(feature_values, feature_pivot, f_col, n=5, agg=np.mean, postfix=''):"""求近邻样本的聚合特征args:feature_values (array): 近邻样本array,维度:(N_NEIGHBORS_MAX, time数量, investment_id数量)feature_pivot (pd.DataFrame): 目标target的pivotf_col (str): 找近邻样本所用的特征n (int): 将n-1个近邻样本的目标target做聚合特征agg (np.agg_method): 聚合的方法postfix (str): 聚合特征命名的后缀return:dst (pd.DataFrame): 聚合特征数据"""pivot_aggs = pd.DataFrame(agg(feature_values[:n-1,:,:], axis=),columns=feature_pivot.columns,index=feature_pivot.index)dst = pivot_aggs.unstack().reset_index()dst.columns = ['investment_id', 'time_id', f'{f_col}_cluster{n}{postfix}_{agg.__name__}']return dst
再导入数据和定义近邻聚合参数配置:
# 导入数据train = pd.read_pickle('./input/train.pkl')train = train.astype(np.float32)#################################### 参数区###################################target_feature = 'target' # 目标变量名p = 2metric = 'minkowski'metric_params = Nonetime_id_neigbor_sizes = [3, 20, 30] # 时间近邻的聚合长度列表time_id_agg_funcs = {'f_1':[np.mean, np.min, np.max, np.std],}# 近邻搜索所用特征合搜索方法N_NEIGHBORS_MAX = max(time_id_neigbor_sizes) # 关注近邻样本的大数量
对训练集,找近邻样本,并做聚合特征:
########################################################## Time维度:基于f_col找近邻样本,并聚合target特征(针对训练集)#########################################################for f_col in time_id_agg_funcs.keys():dsts_list = []# 获取f_col的pivottrain_pivot = train.pivot('time_id', 'investment_id', f_col) # 行:time_id, 列:investment_idtrain_pivot = train_pivot.fillna(train_pivot.mean())train_pivot = pd.DataFrame(minmax_scale(train_pivot), # 时间-along做minmax_scalecolumns=train_pivot.columns,index=train_pivot.index)# 获取target的pivotfeature_pivot = train.pivot('time_id', 'investment_id', target_feature)feature_pivot = feature_pivot.fillna(feature_pivot.mean())# 遍历每个时间点,选择这个时间点前的数据做近邻搜索空间time_id_num = len(train_pivot.index)start_time_idx = N_NEIGHBORS_MAX + 10 # 让搜索空间更大一些for time_idx in tqdm(range(start_time_idx, time_id_num)):nn = NearestNeighbors(n_neighbors=N_NEIGHBORS_MAX, # 查询k个近邻的数目p=p, # 1是曼哈顿距离,2是欧式距离metric=metric, # 距离度量方法,默认'minkowski'metric_params=metric_params, # 评估函数的其它关键参数n_jobs=-1)nn.fit(train_pivot.iloc[:time_idx,:])# 返回近邻样本的 距离 和 索引位置 (time数量,N_NEIGHBORS_MAX)_, neighbors = nn.kneighbors(train_pivot.iloc[[time_idx],:], return_distance=True)# 对时间维度上的近邻样本的target数据, 按距离顺序,排序写入feature_valuestarget_pivot = feature_pivot.iloc[:time_idx,:]feature_values = np.zeros((N_NEIGHBORS_MAX, 1, target_pivot.shape[1]))for i in range(N_NEIGHBORS_MAX):feature_values[i, :] += target_pivot.values[neighbors[:, i], :]has_dsts = Falsedsts = pd.DataFrame()# 便利不同的聚合方法for agg_func in time_id_agg_funcs[f_col]:# 遍历不同的聚合维度for n in time_id_neigbor_sizes:# 对目标变量的近邻样本做聚合特征dst = make_nn_feature(feature_values, train_pivot.iloc[[time_idx],:], f_col, n=n, agg=agg_func, postfix='time')# 列合并当前的聚合特征if has_dsts == False:dsts = copy.deepcopy(dst)has_dsts = Trueelse:dsts = pd.merge(dsts, dst, on=['investment_id', 'time_id'], how='left')dsts_list.append(dsts)# 将聚合特征拼接到原数据集上all_dsts = pd.concat(dsts_list, axis=)train = pd.merge(train, all_dsts, on=['investment_id', 'time_id'], how='left')# 因为train开头有部分数据集因时间长度不够,导致统计值为NaN,这里要drop掉train = train.dropna()
训练集新增近邻聚合特征后:

针对测试集,我们是单步做近邻聚合特征:
########################################################## Time维度:基于f_col找近邻样本,并聚合target特征(针对测试集)#########################################################train = pd.read_pickle('./input/train.pkl')train = train.astype(np.float32)all_df = pd.concat([train, test_df], axis=)for f_col in time_id_agg_funcs.keys():# 获取f_col的pivotall_pivot = all_df.pivot('time_id', 'investment_id', f_col) # 行:time_id, 列:investment_idall_pivot = all_pivot.fillna(all_pivot.mean())all_pivot = pd.DataFrame(minmax_scale(all_pivot), # 时间-along做minmax_scalecolumns=all_pivot.columns,index=all_pivot.index)# document: https://scikit-learn.org/dev/modules/generated/sklearn.neighbors.NearestNeighbors.html#sklearn.neighbors.NearestNeighborsnn = NearestNeighbors(n_neighbors=N_NEIGHBORS_MAX, # 查询k个近邻的数目p=p, # 1是曼哈顿距离,2是欧式距离metric=metric, # 距离度量方法,默认'minkowski'metric_params=metric_params, # 评估函数的其它关键参数n_jobs=-1,)nn.fit(all_pivot)# 返回近邻样本的 距离 和 索引位置 (time数量,N_NEIGHBORS_MAX)test_pivot = all_pivot[all_pivot.index == test_time_id]_, neighbors = nn.kneighbors(test_pivot, return_distance=True)# 获取target的pivotfeature_pivot = all_df.pivot('time_id', 'investment_id', target_feature)feature_pivot = feature_pivot.fillna(feature_pivot.mean()) # 对unseen time一列填充均值feature_pivot = feature_pivot.fillna() # 对unseen investment一行填充均值,即0# 对时间维度上的近邻样本的target数据, 按距离顺序,排序写入feature_valuesfeature_values = np.zeros((N_NEIGHBORS_MAX, 1, feature_pivot.shape[1]))for i in range(N_NEIGHBORS_MAX):feature_values[i, :] += feature_pivot.values[neighbors[:, i], :]# 遍历不同的聚合方法for agg_func in time_id_agg_funcs[f_col]:# 遍历不同的聚合维度for n in time_id_neigbor_sizes:# 对目标变量的近邻样本做聚合特征dst = make_nn_feature(feature_values, test_pivot, f_col, n=n, agg=agg_func, postfix='time')# 将聚合特征拼接到原数据集上test_df = pd.merge(test_df, dst, on=['investment_id', 'time_id'], how='left')
测试集新增近邻聚合特征后:

在用在Ubiquant数据集上,并没有收获到提升,猜测原因如下:
1. Ubiquant使用线上测试API做结果评估,后期的数据距离训练集仍有一段时间距离,参考较远历史的数据,对股票收益率的预测来说,意义可能不大,因为没法rolling的利用target,尽管我们试过递归加入预测值进近邻搜索的样本的空间,但效果更差。
2. 测试集存在训练集不可见的股票资产,这也意味它们在历史的搜索空间内找不到合适/没有近邻样本。
但据队友反馈,在能被rolling的真实业务数据集中,近邻样本聚合特征的加入会有帮助。所以也建议当出现以下类型数据集时,可以考虑试试该特征工程:
1. 测试集预测长度较短,因为过长的话,近邻样本的参考性会减弱;
2. 测试集中unseen对象少些,因为unseen对象缺失近邻搜索空间;
3. 预测目标不会过度依赖短期历史的表现,因为能更好发挥近邻样本聚合特征的特性,不然窗口小的滑窗统计特征便能满足基本需求。
其实,前面近邻样本聚合特征工程代码还能进行一些扩展和改进,比如:
1. 限定搜索空间的大长度,避免搜到过远的近邻样本;
2. 基于近邻距离/顺序,加权聚合;
3. 现在是基于单特征找近邻样本,可以考虑特征组合,找近邻样本;
另外,其实在Transformer类的时序深度模型里,attention layer便扮演着近邻样本搜索的角色,只不过在GBDT类或MLP的模型上,从特征工程的角度,能在一定程度上增加模型对更细粒度的近邻样本学习,而不是简单对全局相似样本的学习。
参考资料
[1] 1st Place Solution - Nearest Neighbors - nyanp,讨论链接:https://www.kaggle.com/competitions/optiver-realized-volatility-prediction/discussion/274970
[2] 1st place (public 2nd place) solution - nyanp,代码链接:https://www.kaggle.com/code/nyanpn/1st-place-public-2nd-place-solution
