在大学阶段,大家都学过概率统计,那么为什么在机器学习中需要使用这部分知识时,却难以支撑了呢?这是我总结的以下几点原因,相信你也曾感同身受。
,大学课程中的内容并没有完全覆盖机器学习领域所需知识点。 机器学习数学基础萌发于高等数学、线性代数和概率统计,但绝不等同于大学本科的教学内容。回想一下大学概率统计课程包含了什么?事件的概率、随机变量及其分布、数字特征、参数估计与假设检验。差不多就这些,很重要、很核心,但这是远远不够的吧。事实上,我们还需要补充随机过程、随机理论、蒙特卡洛思想、采样方法和概率图等一些重要的基础知识,才能构建相对完整的知识结构。
第二,大学课程的学习重计算技巧,轻内在逻辑。大家一定还记得,我们在学习概率统计的时候,首先罗列的就是多种分布,然后算期望、算方差、算事件概率。这样的结果就是数学变成了算术,而且还是在不停重复程序一秒钟就能做好的事。至于知识背后的内在逻辑和应用方法,我们在学习过程中是非常欠缺的,因此大家很容易用完就忘。
第三,虽然我们在大学学了概率统计这门课,却不知道学了能干什么。几十年如一日的教学内容没能深刻挖掘学科与当下前沿技术的交汇点,使得同学们常常有这样的困惑:这门课学了之后有什么用?于是在学完之后,很快就还给老师了。大学开设这门课的目的是讲授概率统计的基础理论,目的并不是为大家打牢机器学习的数学基础。因此,如果我们不能有针对性地分清重点、强化相关重点内容的学习,自然会不明所以。
这么一来,仅凭借大学课程来打好机器学习概率统计的基础,恐非易事。
怎么办?《机器学习中的数学:概率统计》专栏,应运而生,专门为你准备!
这个专栏将如何帮你打好概率统计基础?
《机器学习中的数学:概率统计》和其他数学课程有何不同?这里,我有必要介绍一下这个专栏的特色。
首先,我们会集中力量、紧紧围绕机器学习核心算法中所涉及到的概率统计知识展开介绍,做好打击。我们的讲解会结合数学的本质内涵,用浅显易懂的语言讲透深刻的数学思想,构建起整个理论体系。
然后,我们会加强基础知识与算法、应用案例之间的联系。 我们在讲解概率统计内容的时候会注重延伸后续的算法应用场景,将其进行相互关联,形成学以致用的实践导向。
同时,我们会运用好 Python 工具,做到和工程应用无缝对接。整个专栏内容都以 Python 语言为工具进行教学内容的实践,利用 Numpy、Scipy、Matplotlib、Pandas 等工具强化知识的理解、提升工作效率。
另外,我们还十分重视专栏本身的写作技巧。深入浅出的讲解技巧和逻辑严密的写作文风也将助你在充满挑战的学习道路上不断前进。
专栏大纲与编排思路
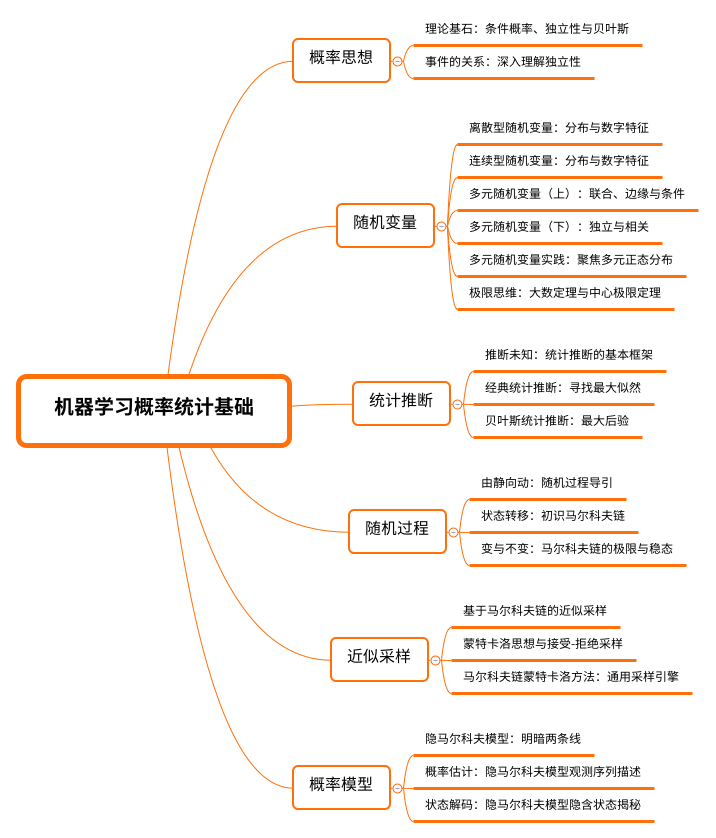
专栏首先从条件、独立、联合、边缘以及贝叶斯思维入手,建立概率统计的理论基石。然后围绕单一变量和多元变量,讨论随机变量这一重点内容,详细讲解变量的分布、多元变量的独立相关性等主干知识,并揭示大数定律、中心极限定理等极限思维和实践方法。紧接着从经典统计推断和贝叶斯推断两大学派介绍统计推断的基本框架。随后讨论随机过程,重点围绕马尔科夫过程展开。并在贯穿蒙特卡洛方法的思想基础上,利用马尔科夫链进行随机采样。后讲解典型的概率图模型隐马尔可夫模型,作为这一部分的结尾。
本专栏将围绕以下六大部分展开
第 1 部分:概率思想。我们首先从条件概率和贝叶斯方法入手,阐明条件、独立、相关等基本概念,掌握联合、边缘的计算方法,我们将一起构建起认知世界的概率思维体系。
第 2 部分:随机变量。我们将重点介绍随机变量主干内容,从单一随机变量的分布过渡到多元随机变量的分析,后重点阐述大数定理和中心极限定理,并初步接触蒙特卡洛方法,和读者一起建立重要的极限思维。
第 3 部分:统计推断。这部分我们关注的是如何通过部分的样本集合推断出我们关心的总体特征,这在现实世界中非常重要。在参数估计的思想方法基础上,我们重点关注极大似然估计和贝叶斯估计这两种方法。
第 4 部分:随机过程。我们将关注由一组随机变量构成的集合,即随机过程。股票的波动、语音信号、视频信号、布朗运动等都是随机过程在现实世界中的实例。我们在随机过程的基本概念之上,将重点分析马尔科夫链,梳理其由静到动的演变,探索变化的过程和不变的稳态。
第 5 部分:采样理论。我们将重点关注如何获取服从目标分布的近似采样方法,从基本的接受-拒绝采样入手,逐渐深入到马尔科夫链-蒙特卡洛方法,通过动态的过程进一步深化对随机过程、随机理论以及极限思想的理解。
第 6 部分:概率模型。这里我们将介绍概率图模型中的一种典型模型:隐马尔科夫模型,熟悉状态序列的概率估计和状态解码的基本方法,为后续学习的概率图模型打好基础。
让我们一起开始这段学习旅程!
万丈高楼平地起,希望《机器学习中的数学》系列专栏能陪伴大家走好机器学习的学习与实践的必经之路、梳理纷繁复杂的知识网络、构筑好算法模型的数学基础。更重要的是,我希望我们能一起形成一种思维习惯:源于理论,我们条分缕析;面向实践,我们学以致用。有了扎实的数学理论和方法基础,相信同学们都能登高望远、一往无前。
