引子
问题:给定一串数字{1,2,5,7,15,24,33,52},如何在时间复杂度为O(1)下,对数据进行CURD?
数组:我创建一个Length为53的数组,将元素插入相同下标处,是不是就可以实现查找复杂度O(1)了?但是添加修改元素时间复杂度为O(n)了。
链表:添加删除复杂度为O(1),但是查找时间复杂度为O(n)了。
身为.NETer肯定熟练使用Dictionary和HashSet,这两个容器的底层就是HashTable,所以带着对技术浓重的兴趣(面试),所以就从头到尾梳理一下!
理论
链地址法(拉链法)
回到问题本身,我们用数组可以实现查找复杂度为O(1),链表实现添加删除复杂度为O(1),如果我们将两个合起来,不就可以实现增删查都为O(1)了么?如何结合呢?
我们先定义一个数组,长度为7(敲黑板,思考下为什么选7?),将所有元素对7取余,这样所有元素都可以放在数组上了,如下图所示:
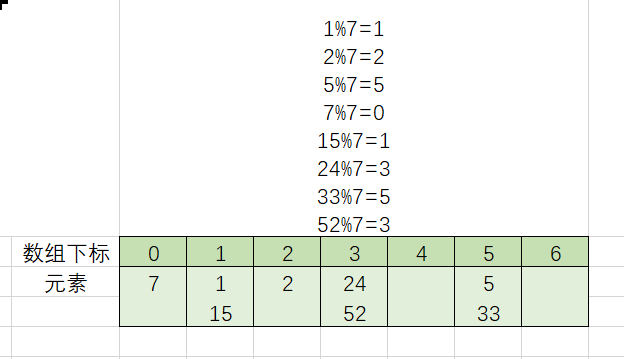
如上图,如果我们将数组中每个下标位置都放成一个链条,这样,复杂度不久降下去了么?
有问题么?没问题。真没问题么?有问题......
注意
插入元素是{0,7,14,21,28}怎么办?这样都落在下标为0的链条里,时间复杂度不又上去了?针对这种情况,隔壁Java将链表优化成了红黑书,我们.NET呢?往下看。
如果我的数组长度不是7,是2怎么办?所有数对2取余,不是1就是0,时间复杂度不又上去了?所以我们对数组长度应该取素数。
如果元素超级多或者特别少,我们的数组长度要固定么?就要动态长度
上边这种方法学名就叫拉链法!
开放地址法
上边我们聊过拉链法(为什么老想着裤子拉链......),拉链法是向下开辟新的空间,如果我们横向开辟空间呢?还是刚才的例子,我们这样搞一下试试。
线性探测法
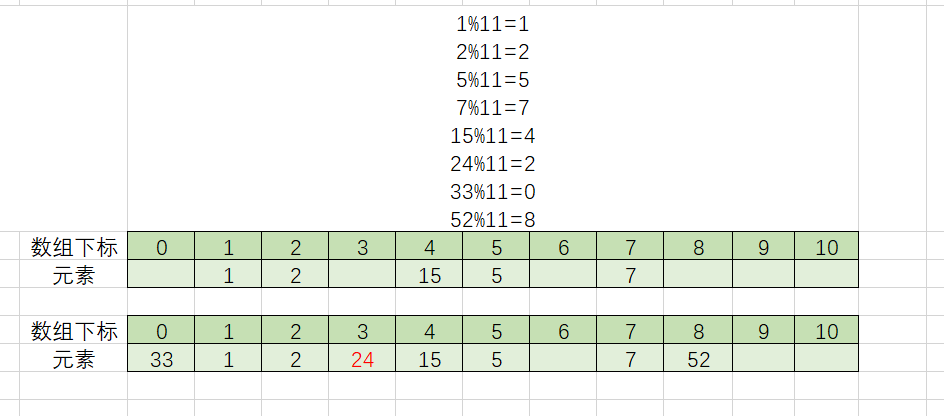
我们插完7以后,在插24时,发现下标为2的地方有元素了,于是向后移动一位,发现有空位,于是就插进去了。
上边这种方法就是线性探测法!
二次聚集(堆积)
聪明的老鸟们,肯定疑惑啦,如果我们继续添加元素{x%11=4},{y%11=5},此时x,y元素都要往下标6插数据。这样就导致了原始哈希地址不同的元素要插入同一个地址。即添加同义词的冲突过程中又添加了非同义词的冲突。这就是二次聚集。
二次探测法
如果在线性探测法中,我们不依次寻找下一个呢?我们针对"下一个"采取{1 ^ 2,-1 ^ 2,2 ^ 2,-2 ^ 2....}(垃圾编辑器,次方样式乱了)这样的步长呢?真聪明!你已经知道二次探测法了!
这......这还能用么?不都乱了么?下标和元素对不上了呀!怎么去查找元素呢?
别急呀,家人们呐,我们按照这个思路查询就好了:
查找算法步骤
1. 给定待查找的关键字key,获取原始应该插入的下标index
2. 如果原始下标index处,元素为空,则所查找的元素不存在
3. 如果index处的元素等于key,则查找成功
4. 否则重复下述解决冲突的过程
* 按照处理冲突的方法,计算下一个地址nextIndex
* 若nextIndex为空,则查找元素不存在
* 若nextIndex等于关键词key,则查找成功
还有要注意的点么?必须有!
注意(敲重点啦)
- 数组长度必须大于给定元素的长度!
- 当数组元素快装满时,时间复杂度也是O(n)!
- 如果都装满了,就会一直循环找空位,我们应该进行扩容!
理论小结
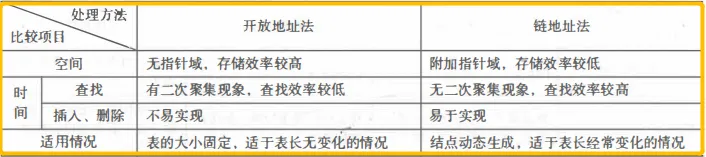
接口设计
干活啦,干活啦,领导嫌查询效率太低,让设计一种CURD时间复杂度都为O(n)的数据结构。给了接口。接口如下:
internal interface IDictionary<TK, TV> : IEnumerable<KeyValuePair<TK, TV>>
{
TV this[TK key] { get; set; }
int Count { get; }
/// <summary>
/// 根据key判断元素是否存在
/// </summary>
/// <param name="key"></param>
/// <returns></returns>
bool ContainsKey(TK key);
/// <summary>
/// 添加元素
/// </summary>
/// <param name="key"></param>
/// <param name="value"></param>
void Add(TK key, TV value);
/// <summary>
/// 根据key移除元素
/// </summary>
/// <param name="key"></param>
void Remove(TK key);
/// <summary>
/// 清除
/// </summary>
void Clear();
}
.NET实现线性探测法
实现过程
1. 先来个对象,存储key和value
对象:KeyValuePair
2. 来个类OpenAddressDictionary,继承IDictionary接口,就是我们的实现类
实现类:OpenAddressDictionary
3.如何实现查找?跟着上文查找步骤就行
线性探测:查找
4. 添加
线性探测:添加
5. 删除
线性探测:删除
终代码
线性探测:终代码
.NET实现拉链法
实现过程
回想一下,上边的拉链法,每个下标位置放置的是一个链条,所以我们先实现一个双向链表
1. 实现一个双向链表
拉链法:构建双向链表
2. 创建一个拉链法实体类
拉链法:实现类
3. 拉链法:查找
拉链法:查找
4. 拉链法:添加
拉链法:添加
5. 拉链法:删除
拉链法:删除
终代码
拉链法:终代码
Dictionary源码分析
模拟实现:一个Dictionary,存储数据{1,'a'},{'4','b'},{5,'c'}
1. 创建一个单链表,用来存储K-V
private struct Entry
{
public uint hashCode;
//值为-1,表示是该链条后一个节点
//值小于-1,表示已经被删除的自由节点
public int next;
public TKey key; // Key of entry
public TValue value; // Value of entry
}
2. 创建一个数组当桶,还有一个链表数组(核心就这两个数组)
private int[]? _buckets;
private Entry[]? _entries;
3. 模拟实现插入{1,'a'},{'4','b'},{5,'c'}
初始化
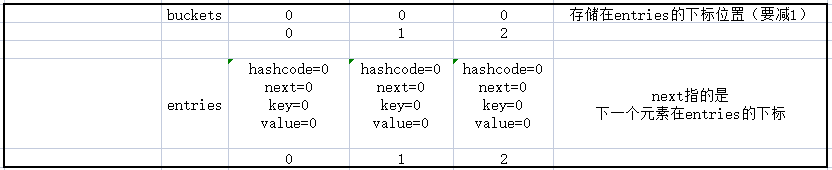
次插入{1,'a'}
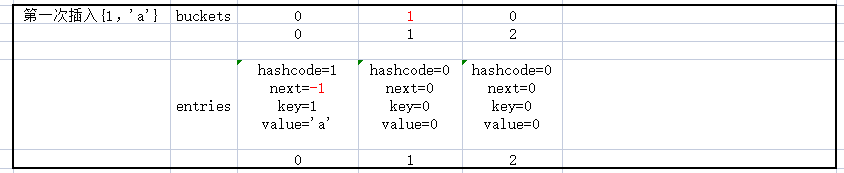
第二次插入{'4','b'}
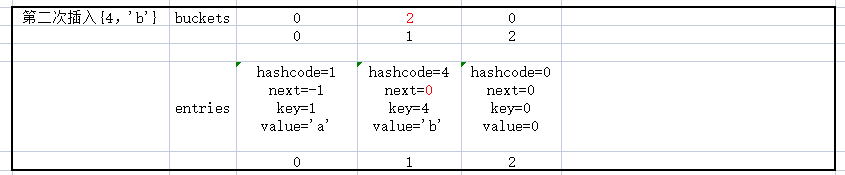
第三次插入{5,'c'}

仔细看一下这三个数据的插入,及数据的变化,应该可以理解_buckets和_entries的关系
4.删除
上边再讲哈希表,包括我们自己实现的代码中,删除一个节点后,都要重新计算后边的位置。如何解决这个问题呢?我们可以使用Entry的next,来表示是否已经删除,小于0就表示是自由节点。
关于删除就这样几个变量:
private int _freeList;//后一个删除的Entry下标
private int _freeCount;//当前已删除,但是还未重新使用的节点数量
private const int StartOfFreeList = -3;//帮助寻找自由节点的一个常量
看一下StartOfFreeList和_freeList和Entry.next如何寻找自由节点
- 删除时:Entry[i].next=上一层中的StartOfFreeList-_freeList
- 添加&&_freeCount>0:_freeList=StartOfFreeList - entries[_freeList].next
请看图理解:

